Hành động ma quái ở khoảng cách xa trong miền mất mát

Không phải tất cả các cực tiểu toàn cục của miền mất mát (huấn luyện) đều được tạo ra như nhau.

Ngay cả khi chúng đạt được hiệu suất tương đương trên tập huấn luyện, các giải pháp khác nhau có thể hoạt động rất khác nhau trên tập kiểm tra hoặc trên phân phối ngoài mẫu. Vậy tại sao chúng ta thường tìm thấy các giải pháp “đơn giản” có khả năng tổng quát hóa tốt?

Trong một bài viết trước đây, chúng ta đã lập luận rằng câu trả lời là “điểm kỳ dị” — những điểm mất mát cực tiểu với các tiếp tuyến không xác định rõ ràng. Chính những điểm kỳ dị “khó chịu” nhất có tác động lớn nhất đến quá trình học và tổng quát hóa trong giới hạn của dữ liệu lớn. Chúng hoạt động như các bộ điều chỉnh ngầm làm giảm chiều hiệu dụng của mô hình.

Hình 1. Các điểm kỳ dị trong miền mất mát làm giảm chiều hiệu dụng của mô hình, từ đó lựa chọn các mô hình có khả năng tổng quát hóa tốt hơn.

Ngay cả sau khi viết bài giới thiệu về “lý thuyết học kỳ dị” này, chúng ta vẫn thấy luận điểm này kỳ lạ và phản trực giác. Làm thế nào mà hình học cục bộ của một vài điểm cô lập lại quyết định hành vi toàn cục kỳ vọng trên tất cả các máy học trên miền mất mát? Điều gì giải thích cho “hành động ma quái ở khoảng cách xa” của các điểm kỳ dị trong miền mất mát?

Hôm nay, trong bài viết này chúng ta sẽ tìm cách để giải thích trực quan theo kiểu vật lý cho luận điểm này.

Nó có thể tóm tắt như sau: các điểm kỳ dị chuyển đổi chuyển động ngẫu nhiên ở đáy các bồn mất mát thành quá trình tìm kiếm khả năng tổng quát hóa.

Bước đi ngẫu nhiên trên các tập mất mát cực tiểu

Trước tiên, hãy xem xét giới hạn mà bạn đã huấn luyện quá lâu đến mức chúng ta có thể coi mô hình như bị giới hạn vào một tập các điểm mất mát cực tiểu cố định ¹ 1. Về mặt kỹ thuật, trong lý thuyết học kỳ dị, chúng ta coi miền mất mát thay đổi với mỗi mẫu bổ sung. Ở đây, chúng ta đang xem xét trường hợp miền mất mát bị đóng băng, và các mẫu mới hoạt động như một loại chuyển động ngẫu nhiên dọc theo tập các điểm mất mát cực tiểu.

Đây là cách để hiểu trực quan: giả sử bạn là một người đi bộ ngẫu nhiên sống trên một đường cong nào đó có các điểm kỳ dị (tự giao cắt, điểm nhọn, và những thứ tương tự). Mỗi bước thời gian, bạn đi một bước có độ dài đồng đều theo một hướng ngẫu nhiên có sẵn. Khi đó, các điểm kỳ dị hoạt động như một loại “bẫy”. Nếu bạn ở gần một điểm kỳ dị, bạn có nhiều khả năng đi một bước hướng tới (và qua) điểm kỳ dị hơn là đi một bước ra xa khỏi điểm kỳ dị.

Hình 2. Nếu chúng ta bắt đầu từ điểm màu xanh lam và lấy mẫu ngẫu nhiên vị trí tiếp theo trong số bảy vị trí có sẵn với kích thước bước cố định, chúng ta có tỷ lệ 6:1 có lợi cho việc di chuyển về phía điểm kỳ dị.

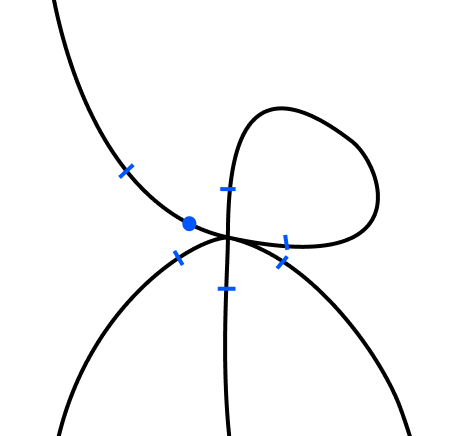
Nó không hoàn toàn là một điểm hút (chúng ta đang trong một thiết lập ngẫu nhiên, nơi bạn vẫn có thể thoát ra khỏi đó thỉnh thoảng), nhưng nó đủ “dính” để điểm kỳ dị “lớn nhất” sẽ chiếm ưu thế trong phân phối ổn định của bạn.

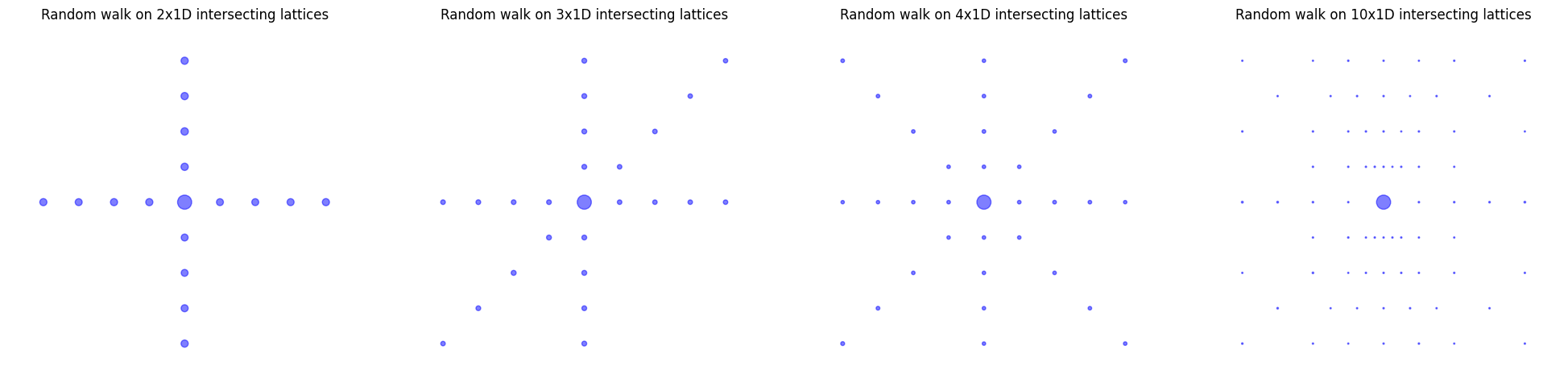
Trong trường hợp rời rạc, đây chỉ là hiện tượng nổi tiếng về việc các nút có bậc cao chi phối phần lớn hành vi kỳ vọng của đồ thị của bạn. Trong kinh doanh, nó là lý do đằng sau sự tồn tại của Google. Trong mạng xã hội, nó tương tự như cách bạn bè trung bình của bạn có nhiều bạn bè hơn bạn.

Để hiểu điều này, hãy xem xét một ví dụ đơn giản: lấy hai đa giác và để chúng giao nhau tại một điểm duy nhất. Tiếp theo, để một người đi bộ ngẫu nhiên chạy tự do trong thiết lập này. Người đi bộ ngẫu nhiên sẽ đi qua mỗi điểm thường xuyên như thế nào?

Hình 3. Lấy hai hoặc nhiều lưới 1D với điều kiện biên hình thỏi và để chúng giao nhau tại một điểm. Trong giới hạn của một đa giác/lưới vô hạn, bạn sẽ có một điểm kỳ dị giao cắt thông thường tại gốc tọa độ.

Nếu bạn đã học một khóa về lý thuyết đồ thị, bạn có thể nhớ rằng phân phối cân bằng đặt trọng số cho các nút tỷ lệ thuận với bậc của chúng. Đối với hai đường thẳng giao nhau, giao điểm có xác suất gấp đôi so với các điểm khác. Đối với ba đường thẳng giao nhau, nó có xác suất gấp ba lần, và cứ tiếp tục như vậy…

Hình 4. Kích thước của hình tròn cho thấy khả năng xuất hiện của điểm đó trong mô phỏng thực nghiệm. Phân phối dừng đặt nhiều trọng số hơn vào gốc tọa độ bằng đúng số lượng đường thẳng giao nhau.

Chuyển động Brown gần tập mất mát cực tiểu

Không hoàn toàn chính xác. Bạn thấy đấy, việc giới hạn chuyển động của chúng ta dọc theo các điểm mất mát cực tiểu là không thực tế. Chúng ta quan tâm hơn đến thực tế hỗn loạn, nơi chúng ta được phép có một số tự do để di chuyển quanh đáy các bồn mất mát. ² 2. Chúng ta vẫn coi miền mất mát là đóng băng nhưng bây giờ sẽ cho phép sự khởi hành ra xa khỏi các điểm mất mát cực tiểu.

Lần này, trực quan quan trọng là xem hành vi của gradient giảm dần ngẫu nhiên trong giai đoạn cuối của quá trình huấn luyện như một loại chuyển động Brown. Khi chúng ta đã đạt được một giải pháp mất mát huấn luyện thấp, sự biến đổi giữa các batch là nguồn ngẫu nhiên không còn cải thiện đáng kể mất mát nữa mà chỉ làm chúng ta lắc lư giữa các giải pháp tương đương nhau từ góc nhìn của tập huấn luyện.

Để hiểu được động lực này, chúng ta có thể nghiên cứu trường hợp trừu tượng hơn của chuyển động Brown trong một miền năng lượng liên tục nào đó với các điểm kỳ dị.

Xét hàm thế năng cho bởi $$ U(\mathbf{x}) = \alpha \cdot \min((x_0 - b^2), (x_1 - b)^2) $$

Hàm này được vẽ ở bên trái của hình dưới đây. Phía bên phải mô tả phân phối ổn định tương ứng được dự đoán bởi vật lý “thông thường”. ³ 3. Tức là: phân phối Gibbs.

Hình 5. Một miền năng lượng có tập mất mát cực tiểu với một điểm kỳ dị giao cắt thông thường tại gốc tọa độ. Điều kiện biên hình thỏi như trong trường hợp rời rạc.

Mô phỏng chuyển động Brown trong hố thế này tạo ra một phân phối thực nghiệm trông khá khác với dự đoán thông thường…

Hình 6. Điểm kỳ dị nhận được xác suất cao hơn nhiều so với những gì bạn mong đợi từ vật lý "thông thường".

Giống như trong trường hợp rời rạc, điểm kỳ dị tại gốc tọa độ thu hút mật độ xác suất, ngay cả ở nhiệt độ hữu hạn và ngay cả đối với các điểm xa khỏi tập mất mát cực tiểu.

Kết luận

Tóm lại, trực quan ⁴ 4. Xin nhấn mạnh: đây chỉ là lời giải thích hình tượng/định tính/theo kiểu vật lý. Đừng coi nó quá nghiêm túc như một mô hình cho những gì SGD thực sự đang làm. Cách “thích hợp” để suy nghĩ về điều này (cảm ơn Dan) là về mật độ các trạng thái. có thể được mô tả như sau: trong trường hợp giới hạn, chúng ta không mong đợi mô hình học được nhiều từ bất kỳ mẫu bổ sung nào. Thay vào đó, sự ngẫu nhiên trong việc lấy mẫu mới hoạt động như chuyển động Brown cho phép mô hình khám phá tập mất mát cực tiểu. Các điểm kỳ dị là một bẫy cho chuyển động Brown này, cho phép mô hình tìm thấy các giải pháp tổng quát hóa tốt chỉ bằng cách di chuyển xung quanh.

Vì vậy, SGD hoạt động hiệu quả vì cuối cùng nó bị mắc kẹt gần các điểm kỳ dị, và các điểm kỳ dị tổng quát hóa tốt hơn.

Bạn có thể tìm thấy mã cho các mô phỏng này tại đây và tại đây.