Mạng neural có khả năng suy rộng là nhờ vào một ''thủ thuật (trick)'' kỳ quặc!!!

Jan. 15, 2025

Lý thuyết Học thống kê đang lừa dối bạn rằng: Các mô hình tham số hóa quá mức (“Overparametrized” models) không thật sự quá mức, và khả năng suy rộng/ tổng quát hóa (generalization) không chỉ là một câu hỏi về độ rộng của lòng chảo trong không gian độ lỗi.

Theo thứ tự đầu tiên, do các lưu vực mất mát (loss basins) không thực sự là lưu vực mà là các thung lũng (valleys) và tại ở đáy của các thung lũng này có những “dòng sông (rivers)” mà có độ mất mát tối tiểu, không đổi. Số chiều của những tập tối tiểu này càng cao, tác động của số chiều của mô hình của bạn càng thấp. ¹ 1. Số chiều của các tham số tối ưu cũng phụ thuộc vào phân phối đúng (phân phối gốc) mà sinh ra phân phối của bạn, nhưng thậm chí là nếu tập các tham số tối ưu là zero-dimensional đi chăng nữa thì sự hiện hữu của các tập mức (level sets) ở một số nơi nào đó vẫn có thể ảnh hướng đến quá trình học (learning process) và khả năng suy rộng/ tổng quát hóa (generalization). . Khả năng suy rộng/ tổng quát hóa là một sự cân bằng giữa khả năng biểu diễn (expressivity, nhiều tác động của tham số) và tính đơn giản (simplicity, ít tác động của tham số)

Thực vậy, chính là các kỳ dị của các tập mất mát tối tiểu - tức là các điểm tại đó mà đường tiếp tuyến không được xác định rõ ràng/ không đặt chỉnh (ill-defined) - quyết định hiệu suất suy rộng của mô hình. Khẳng định đáng chú ý của Lý thuyết Học kỳ dị (tức đối tượng trung tâm của nghiên cứu này) là rằng “Nhìn chung, Tri thức (knowledge) $\dots$ cần được khai phá tương ứng với các kỳ dị” [1]. Các kỳ dị phức tạp giúp cho các hàm đơn giản hơn mà có khả năng suy rộng tốt hơn.

Về mặt lý thuyết cơ học, kết quả của những tập mất mát tối tiểu (minimum-loss sets) này xuất phát từ tính đối xứng nội tại của mạng neural ² 2. Và từ phân phối gốc (true distribution). : các biến thể liên tục của trọng số của một mạng cho trước nhất định phải thực hiện cùng một phép tính. Nhiều tính đối xứng trong số chúng là “tổng quát (generic)” vì chúng được tiền xác định bởi kiến trúc và luôn luôn hiện hữu. Các tính chất đối xứng thú vị hơn là các tính đối xứng “không tổng quát (non-generic)” mà mô hình học có thể tạo ra hoặc phá vỡ trong quá trình huấn luyện.

Về các tính đối xứng không tổng quát (non-generic symmetries) này, một phần sức mạnh của mạng neural là chúng có thể thay đổi hiệu quả số chiều của chúng. Tính suy rộng/ tổng quát đến từ một dạng lựa chọn mô hình nội tại, trong đó mô hình tìm ra các điểm kỳ dị phức tạp hơn nhưng sử dụng ít tham số hiệu quả hơn, từ đó ưu tiên chọn lọc được các hàm đơn giản hơn và có khả năng tổng quát hóa tốt hơn.

$$ \text{Complex Singularities} \Leftrightarrow \text{Fewer Parameters} \Leftrightarrow \text{Simpler Functions} \Leftrightarrow \text{Better Generalization} $$

Với nhiều rủi ro chỉ trích bởi yêu cầu về tính tao nhã, SLT có vẻ là một con đường đầy hứa hẹn để phát triển một lý thuyết cho sự hiểu biết tốt hơn về tính tổng quát hóa/ suy rộng và những giới hạn trong động lực huấn luyện. Nếu ta may mắn, SLT thậm chí có thể giúp chúng ta xây dựng một lý thuyết thống nhất vĩ đại về quy mô mô hình (grand unified theory of scaling)

Vẫn còn rất nhiều việc phải làm (về mặt tính toán thực tế, các nhà lý thuyết vẫn đang mải mê với các mô hình một lớp sử dụng hàm tanh), nhưng từ một khảo sát ban đầu, Lý thuyết Học kỳ dị có vẻ sâu sắc hơn so với các cách giải thích khác về tính tổng quát hóa. Và điều này không chỉ nằm ở sự sâu sắc; có thể nói rằng Lý thuyết Học kỳ dị là một điều kiện tiên quyết không thể thiếu (non-negotiable prerequisite) cho bất kỳ lý thuyết nào về học sâu. Hãy cùng tìm hiểu sâu hơn.

I. Trở lại với Bayes-ics

Lý thuyết học kỳ dị bắt đầu với bốn thành phần cơ bản:

• \(q(x)\) là một số phân phối nào đó mà phát sinh ra các mẫu của chúng ta;
• Một mô hình \(p(x \mid w)\) mà được tham số hóa bởi trọng số \(w \in \mathcal{W} \subset \mathbb{R}^d\) trong đó \(\mathcal{W}\) là một tập compact;
• Một phân phối tiên nghiệm trên các trọng số \(\varphi(w)\);
• Và một tập dữ liệu gồm các mẫu \(D_n = {X_1, \dots, X_n}\) trong đó mỗi biến ngẫu nhiên \(X_i\) i.i.d tương ứng với \(q(x)\).

Mục tiêu ở mức thấp (lower-level) của “learning” là tìm kiếm những trọng số tối ưu cho một tập dữ liệu sẵn có. Đối với lý thuyết Bayesian, điều này có ý nghĩa rất cụ thể và hạn chế:

$$ p(w \mid D_n) = \frac{p(D_n \mid w) \varphi(w)}{p(D_n)}. $$

Còn mục tiêu cao hơn của “learning” là tìm kiếm lớp mô hình/ kiến trúc tối ưu \(p(x \mid w)\) cho một tập dữ liệu sẵn có. Thay vì cố gắng tìm những trọng số sao cho cực đại likelihood hay thậm chí là cực đại posterior, mục tiêu đúng đắn của Bayesian là tìm kiếm mô hình mà cực đại model evidence, tức là:

$$ p(D_n) = \int_\mathcal{W} p(D_n \mid w)\varphi(w)dw. $$

Thật vậy, mô thức Bayesian có thể tích hợp trọng số của nó để đưa ra các nhận định về toàn bộ các lớp mô hình là một trong những điểm mạnh chính của nó. Và thật vậy, tích phân này ~thường~ hầu như luôn luôn khó để giải và đó cũng chính là điểm yếu chính của nó. Thế nên mà Bayesian lựa chọn một hướng giải quyết dựa trên phong cách tần suất với phép tính gần đúng Laplace dễ hiểu hơn nhiều: ta tìm kiếm một lựa chọn của các trọng số $w^{(0)}$ mà cực đại likelihood và sau đó xấp xỉ phân phối như Gaussian ở gần điểm đó.

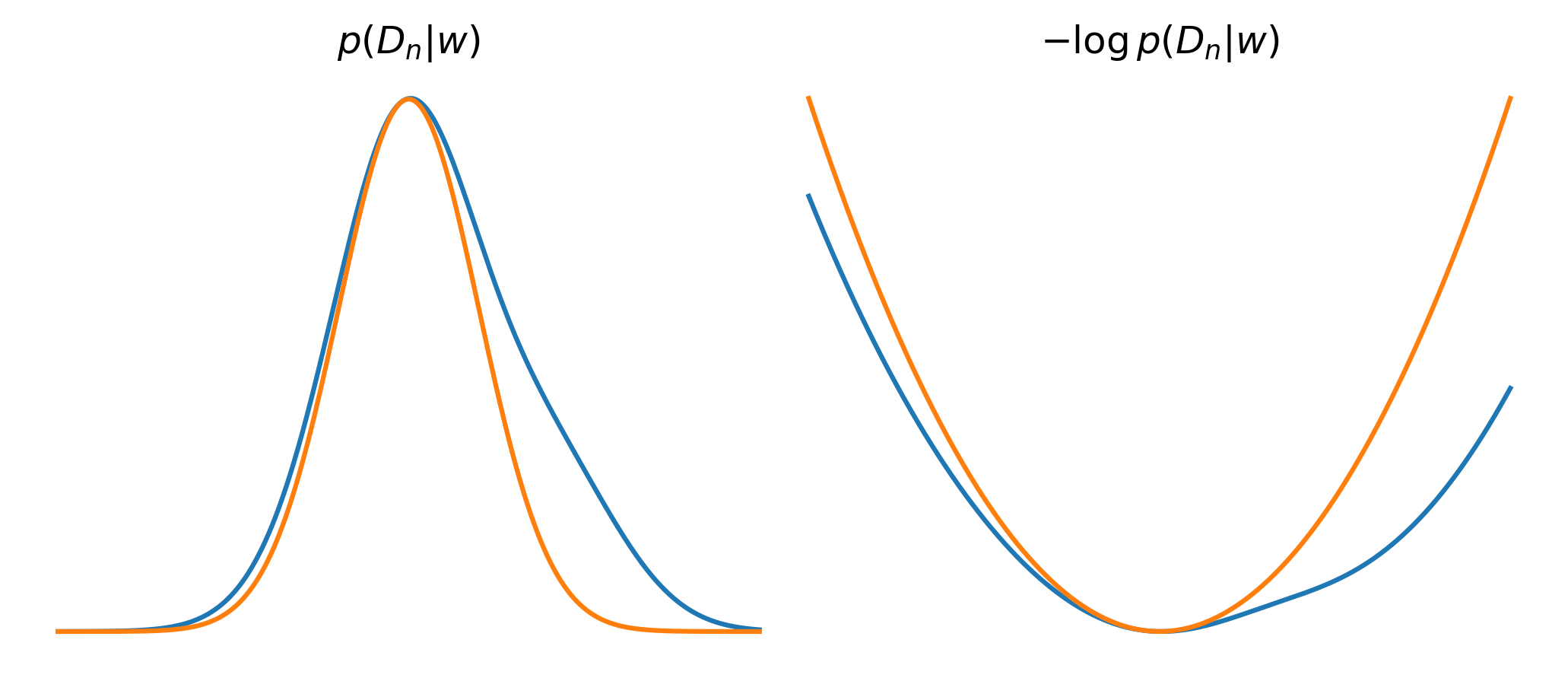
Điều này được chứng minh là hợp lý khi dữ liệu lớn dần $(n \rightarrow \infty)$, nhờ vào định lý giới hạn trung tâm (central limit theorem), phân phối trở nên gần (tiệm cận với) phân phối chuẩn (asymptotically normal) (so sánh với lý thuyết Vật lý và thuật ngữ của họ “mọi thế năng là một hàm điều hòa (harmonic oscillator) nếu ta nhìn nó đủ gần/ tiếp tục hạ nhiệt độ”.)

Từ xấp xỉ này, một ít biến đổi Toán học dẫn dắt chúng ta đến với dạng tiệm cận (asumptotic form) với negative log evidence (khi lấy giới hạn \(n \rightarrow \infty\)) như sau:

$$ -\log p(D_n) \approx \underbrace{-\log p(D_n \mid w_0)} _{accuracy} \quad+\quad \underbrace{\frac{d}{2}\log{n}} _{simplicity}, $$ trong đó \(d\) là chiều của không gian tham số.

Biểu thức này được biết với tên gọi Bayesian Information Criterion (BIC) và nó (khá giống với Akaike information criterion) tạo nên Dao cạo Ockham (Occam’s razor) trong ngôn ngữ của Thống kê Bayesian. Ta có thể chấp nhận dừng lại với các mô hình mà hoạt động kém miễn là chúng đơn giản. Trong ngôn ngữ của phân tích độ phức tạp thuật toán (algorithmic-complexity), BIC có một diễn giải thay thế như một công cụ cho việc tối tiểu độ dài mô tả trong một ngữ cảnh tối ưu mã hóa nào đó.

Thật không may, BIC sai. Hoặc ít nhất là BIC không áp dụng cho bất kỳ mô hình nào mà chúng ta thực sự quan tâm nghiên cứu. Và may mắn thay, lý thuyết học kỳ dị có thể tính toán chính xác dạng tiệm cận và tiết lộ những hàm ý rộng hơn nhiều so với BIC.

II. Lý thuyết học thống kê được xây dựng nên từ một trò lừa dối!

Thông tin trọng yếu trong nghiên cứu của Watanabe là khi mà ánh xạ hàm tham số hóa (parameter-function map) $$ \mathcal{W} \ni w \rightarrow p(\cdot \mid w) $$ không phải là ánh xạ một-đến-một (injective function, đơn ánh), mọi thứ bắt đầu kỳ quặc. Đó là khi mà những lựa chọn khác nhau của các trọng số tạo nên cùng các hàm, các công cụ của lý thuyết học thống kê bị phá sản. Chúng ta gọi những mô hình này là “không có tính xác định” (non-identifiable).

Lấy ví dụ về phép xấp xỉ Laplace. Nếu có một đối xứng liên tục địa phương trong không gian trọng số, tức là một số hướng bạn có thể đi mà không ảnh hưởng đến mật độ xác suất, thì mật độ của bạn không phải là Gaussian địa phương.

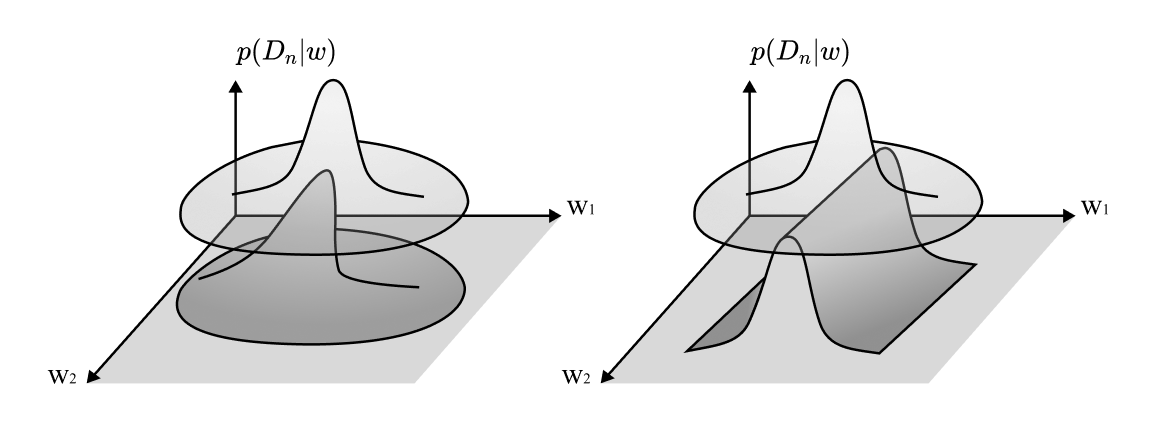
Ngay cả khi các đối xứng không liên tục, nhìn chung, mô hình sẽ không tiệm cận chuẩn tắc (asymptotically normal). Nói cách khác, định lý giới hạn trung tâm chuẩn (standard central limit theorem) không còn đúng!.

Vấn đề tương tự phát sinh nếu bạn đang xem xét tới bề mặt mất mát (loss landscapes) trong một số trình bày quy chuẩn của học máy. Ở đây, bạn sẽ tìm thấy các nỗ lực để đo thể tích lưu vực “basin” bằng cách khớp một parabol với Hessian của loss landscape tại trọng số cuối cùng đã được huấn luyện xong. Đó là một thủ thuật quen thuộc và nó vẫn tiếp tục gặp cùng vấn đề!.

Đây không phải là loại vấn đề mà bạn có thể giải quyết đơn giản bằng cách thêm một \(\epsilon\) nhỏ vào Hessian và coi như xong. Có các cách để khôi phục “thể tích”, nhưng chúng đòi hỏi sự cẩn trọng. Vì vậy, một bài học thực tế ở đây là: nếu bạn thấy mình thêm \(\epsilon\) để làm cho Hessian có thể nghịch đảo, hãy nhận ra rằng các hướng không (zero directions) đó thực sự rất quan trọng để hiểu điều gì đang diễn ra trong mạng học. Hãy dành cho các giá trị riêng đó sự tôn trọng mà chúng xứng đáng nhận được.

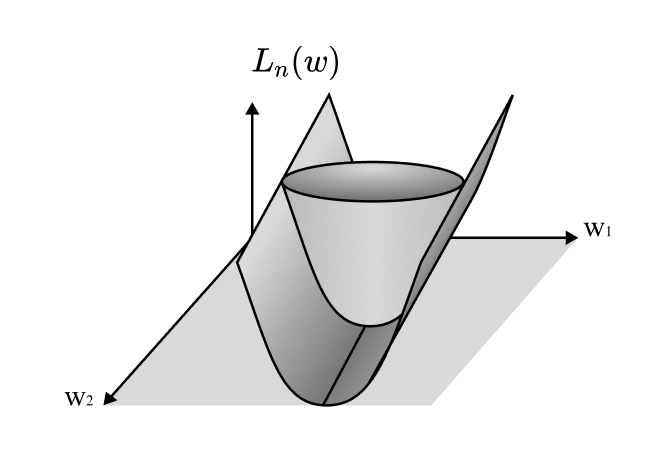
Hệ quả của các giá trị bằng 0 này (và tất nhiên, chúng thực sự tồn tại trong mạng neural) là chúng làm giảm chiều không gian hiệu quả của mô hình. Một bước di chuyển theo các hướng này không làm thay đổi mô hình thực sự đang được triển khai, do đó bạn có ít tham số hơn để “thực hiện các tác vụ”.

Vấn đề cơ bản ở đây là: hầu hết các mô hình mà chúng ta thực sự quan tâm (không chỉ mạng neural mà còn cả mạng Bayesian, mô hình Markov ẩn (HMMs), mô hình hỗn hợp/ mixture models, máy Boltzmann, v.v.) đều chứa đầy các đối xứng, và điều này có nghĩa là chúng ta không thể áp dụng công cụ thông thường của lý thuyết học thống kê được.

III. Learning (Học) là vật lý kết hợp với likelihoods

Bây giờ hãy viết lại biểu thức cập nhật Bayes thân yêu của chúng ta như sau:

$$ p(w \mid D_n) = \frac{1}{Z_n}\varphi(w)e^{-n\beta L_n(w)}, $$ trong đó hàm \(L_n(w)\) là negative log likelihood được định nghĩa như sau:

$$ L_n(w) := - \frac{1}{n}\log p(D_n \mid w) = -\frac{1}{n}\sum_{i=1}^{n}\log p(x_i \mid w), $$ và \(Z_n\) là model evidence, được định nghĩa như sau:

$$ Z_n := p(D_n) = \int_\mathcal{W}\varphi e^{-n\beta L_n(w)}dw. $$

Để ý rằng chúng ta “lé lút” thêm vào một nghịch đảo “nhiệt lượng” (inverse temperature) \(\beta > 0\) thế nên giờ đây chúng ta đang nằm trong tempered Bayes paradigm [4].

Mục tiêu hiện tại của thay đổi này là để nhấn mạnh mối liên hệ với Vật lý, trong đó \(Z_n\) là một ký hiệu quen thuộc (và “hàm phân hoạch/ partition function” là tên gọi của nó). Tương tự lý thuyết thông tin của hàm phân vùng là năng lượng tự do (free energy): $$ F_n := -\log Z_n, $$ mà sẽ là đối tượng nghiên cứu trung tâm của chúng ta.

Dưới định nghĩa của Hamiltonian (hay “hàm năng lượng/ energy function”), ta có: $$ H_n(w) := nL_n(w) - \frac{1}{\beta}\log \varphi(w), $$

Mối liên hệ giờ đây đã hoàn thiện: Lý thuyết Học thống kê thực chất là Vật lý Toán, trong đó Hamiltonian là một quá trình ngẫu nhiên được xác định bởi xác suất likelihood và phân phối tiên nghiệm (prior distribution). Cũng giống như Hình học của bề mặt năng lượng mà quyết định hành vi của các hệ thống Vật lý mà chúng ta nghiên cứu, Hình học của log-likelihood sẽ quyết định hành vi của các hệ thống học mà chúng ta nghiên cứu.

Trong cách diễn giải Vật lý này, một phân phối hậu nghiệm (posteriori distribution) là trạng thái cân bằng (equilibrium state) gắn liền với Hamiltonian thực nghiệm (empirical Hamiltonian). Ý nghĩa của năng lượng tự do (free energy) nằm ở chỗ giá trị tối thiểu của năng lượng tự do — chứ không phải Hamiltonian — mới quyết định trạng thái cân bằng.

Bước tiếp theo là chuẩn hóa các đại lượng quan tâm này để ta có thể dễ làm việc với chúng hơn. Đối với negative log likelihood, việc chuẩn hóa có nghĩa là trừ đi giá trị tối thiểu (minimum value) của nó. ³ 3. Cần làm rõ rằng việc chuẩn hóa này dựa trên giả định về tính khả thi (assumption of realizability) — nghĩa là tồn tại một số trọng số \(w_0\) sao cho \(p(x \mid w_0)\) bằng với \(q(x)\) gần như ở mọi nơi. Với giả định này, giá trị tối thiểu của negative log likelihood tương ứng với entropy thực nghiệm của hệ thống.

Nhưng điều đó chỉ cho ta KL divergence (phân kỳ KL): $$ K_n(w) = L^0_n(w) := L_n(w) - S_n = \frac{1}{n}\sum_{i = 1}^n\log \frac{q(X_i)}{p(X_i \mid w)}, $$ trong đó \(S_n\) là entropy thực nghiệm được định nghĩa như sau: $$ S_n := -\frac{1}{n}\sum_{i = 1}^n\log q(X_i), $$ Dễ thấy, entropy thực nghiệm là một thành phần độc lập với \(w\).

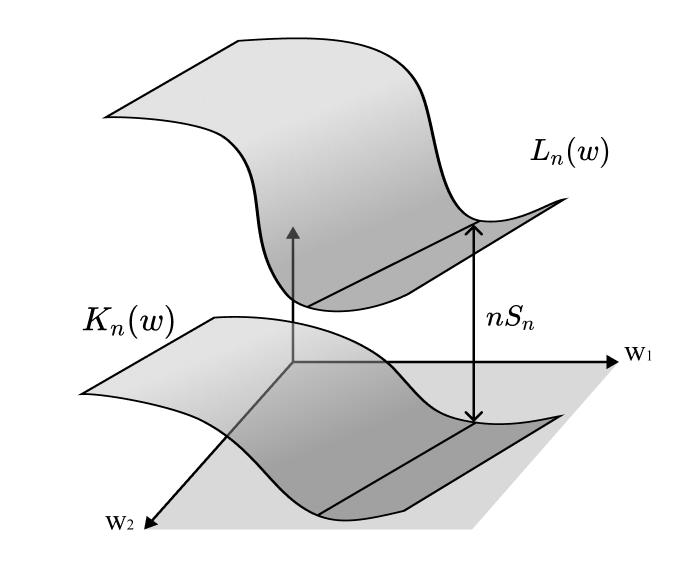
Tương tự, ta chuẩn hóa hàm phân hoạch để có được: $$ Z^0_n = \frac{Z_n}{\prod_{i=1}^n q(X_i)^\beta}. $$ và chuẩn hóa năng lượng tự do để có được: $$ F^0_n = -\log Z^0_n. $$

Điều này cho phép viết lại phân phối hậu nghiệm như sau: $$ p(w \mid D_n) = \frac{1}{Z^0_n}\varphi(w)e^{-n\beta K_n(w)}. $$

Mục tiêu quan trọng của quá trình biến đổi này là làm cho các điểm cực tiểu của biểu thức trong số mũ, \(K(w)\), bằng 0. Nếu chúng ta tìm được cách biểu diễn \(K(w)\) dưới dạng một đa thức, điều này cho phép chúng ta tận dụng công cụ mạnh mẽ của Hình học Đại số (Algebraic Geometry) - một lĩnh vực nghiên cứu các nghiệm của đa thức. Nhờ vậy, chúng ta đã chuyển vấn đề từ trong Lý thuyết Xác suất và Thống kê thành một vấn đề của Đại số và Hình học.

IV. Tại sao lại “singular” (kỳ dị)?

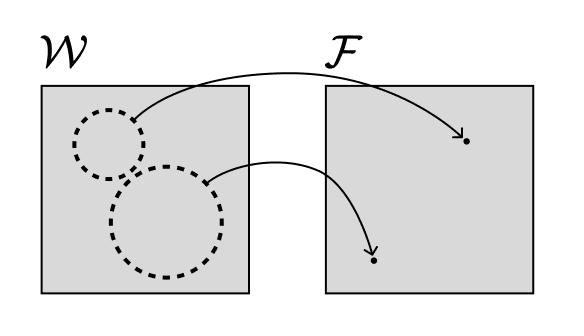
Lý thuyết học “kỳ dị” được gọi là “kỳ dị” vì các “điểm kỳ dị” (nơi tiếp tuyến không được xác định rõ/ không đặt chỉnh - ill-defined) của tập hợp các cực tiểu của hàm mất mát của chúng ta, $$ \mathcal{W}_0 := { w_0 \in \mathcal{W} \mid K(w_0) = 0}, $$ quyết định dạng tiệm cận (asymptotic form) của năng lượng tự do. Về mặt Toán học, \(\mathcal{W}_0\) là một algebraic variety/ đối tượng đại số mà thực chất là một đa tạp (manifold) có thể bao gồm các điểm kỳ dị, nơi nó không cần phải có cấu trúc Euclid địa phương (locally Euclidean).

Hiển nhiên, thật rất khó khăn để nghiên cứu các đối tượng đại số này khi gần các điểm kỳ dị của chúng. Để làm được điều đó, chúng ta cần “giải quyết các điểm kỳ dị” (resolve the singularities). Điều này được thực hiện bằng cách xây dựng một đối tượng hình học mới, có cấu trúc tốt hơn, mà “bóng” của nó chính là đối tượng ban đầu, sao cho hệ thống mới này giữ được tất cả các đặc điểm quan trọng của hệ thống ban đầu.

Hãy xem hình minh họa sau đây để hiểu rõ hơn. Ý tưởng chính đằng sau việc giải quyết điểm kỳ dị là tạo ra một đa tạp mới \(\mathcal{U}\) và một ánh xạ \(g: \mathcal{U} \rightarrow \mathcal{W}\), sao cho \(K(g(u))\) là một đa thức trong các tọa độ địa phương của \(\mathcal{U}\). Chúng ta “gỡ rối” các điểm kỳ dị để trong hệ tọa độ mới để mà chúng giao nhau theo cách “bình thường”.

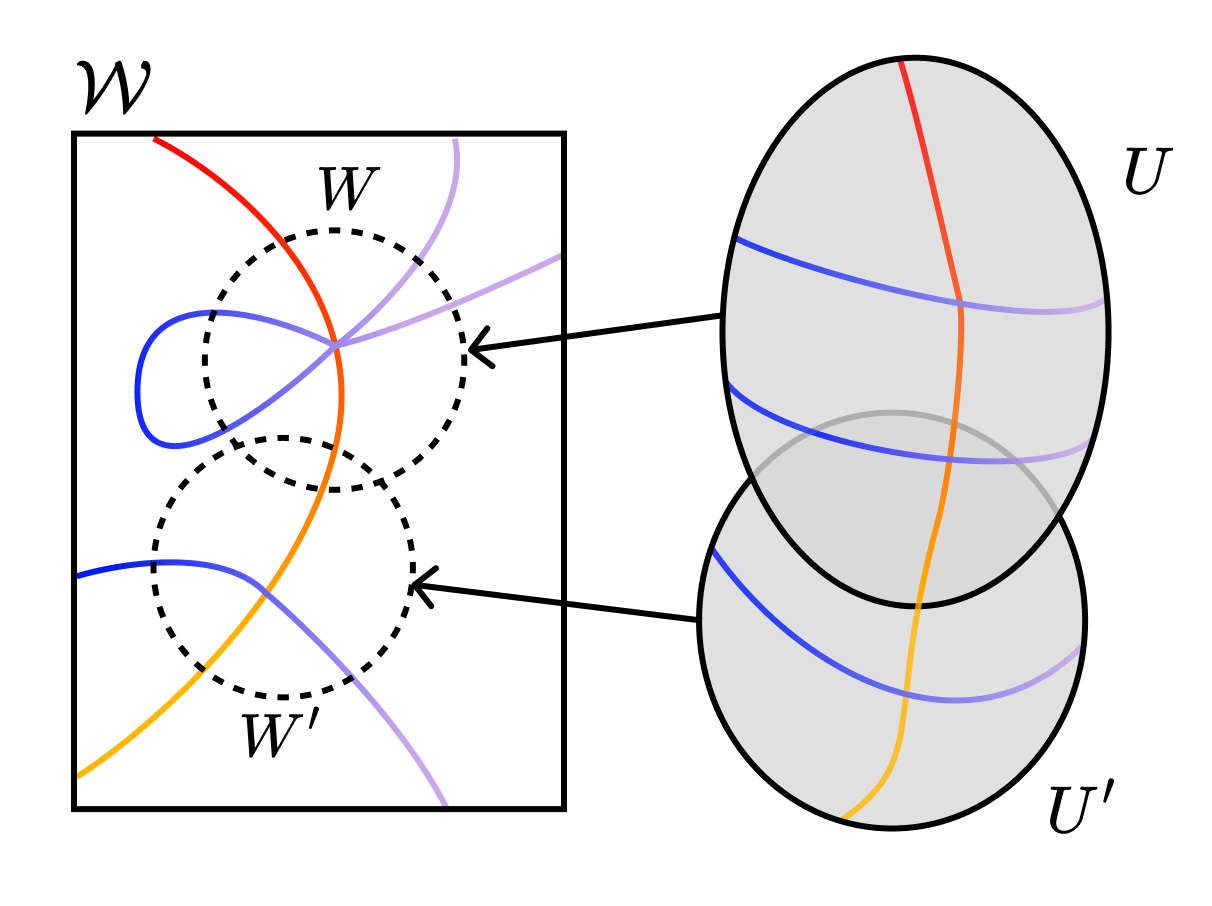
Do việc “thổi phồng” (blow up) tạo ra một đối tượng mới, chúng ta cần cẩn thận để đảm bảo rằng các đại lượng đo lường cuối cùng không thay đổi theo phép ánh xạ—chúng ta cần tìm các bất biến song tỉ (birational invariants).

Một bất biến song tỉ mà chúng ta đặc biệt quan tâm là ngưỡng chuẩn tắc log thực (RLCT - Real Log Canonical Threshold). Nói một cách đơn giản, RLCT đo lường mức độ “tồi tệ” của một điểm kỳ dị. Chính xác hơn, nó đo lường “chiều không gian hiệu quả” gần điểm kỳ dị đó.

Sau khi điều chỉnh định lý giới hạn trung tâm để áp dụng được cho các mô hình kỳ dị, Watanabe đã dẫn xuất dạng tiệm cận của năng lượng tự do khi \(n \rightarrow \infty\): $$ F_n = n\beta S_n + \lambda\log n - (m -1)\log\log n + F^R(\xi) + o_p(1), $$ trong đó \(\lambda\) là RLCT, \(m\) là “multiplicity” gắn với RLCT, \(F^R(\xi)\) là một (well-behaved) biến ngẫu nhiên, and \(o_p(1)\) là một biến ngẫu nhiên mà hội tụ (theo nghĩa Xác suất) về không.

Quan sát quan trọng ở đây là hành vi toàn cục của mô hình bị chi phối bởi hành vi địa phương tại các điểm kỳ dị “tồi tệ nhất” của nó.

Đối với các mô hình thông thường (= không kỳ dị), RLCT là \(d/2\), và với lựa chọn nhiệt nghịch đảo phù hợp, công thức trên trở nên đơn giản: $$ F_n \approx nS_n + \frac{d}{2}\log n \quad\text{(for regular models)}, $$

Như kỳ vọng, đây chính là BIC (Bayesian Information Criterion)!.

Công thức năng lượng tự do này khái quát hóa BIC từ Lý thuyết Học cổ điển sang Lý thuyết Học kỳ dị, trong đó lý thuyết học thông thường là một trường hợp đặc biệt. Chúng ta thấy rằng các điểm kỳ dị hoạt động như một dạng điều chuẩn ngầm (implicit regularization), phạt các mô hình có chiều không gian hiệu quả cao hơn.

V. Sự chuyển pha là các thao tác kỳ dị!

Cực tiểu hóa năng lượng tự do đồng nghĩa với việc cực đại hóa bằng chứng mô hình (model evidence) - mà như chúng ta đã biết thì đó chính là cách tiếp cận được ưa chuộng trong Bayesian để lựa chọn mô hình. Các phong cách (paradigms) khác có thể không đồng tình với điều này ⁶ 6. Tất nhiên, họ sai. , nhưng ít nhất đối với chúng ta, điều này khiến việc cực tiểu năng lượng tự do trở thành mục tiêu trung tâm của Học thống kê.

Giống như trong Học thống kê, trong Vật lý cũng vậy.

Trong các hệ vật lý, chúng ta phân biệt giữa trạng thái vi mô (microstates) như vị trí và vận tốc cụ thể của từng hạt trong một chất khí, với trạng thái vĩ mô (macrostates) như giá trị của thể tích và áp suất. Việc ánh xạ từ trạng thái vi mô sang trạng thái vĩ mô không phải là một đơn ánh chính là điểm khởi đầu của Vật lý Thống kê: các phân phối đồng nhất (uniform distributions) trên trạng thái vi mô dẫn đến các phân phối thú vị hơn trên trạng thái vi mô.

Thường thì, chúng ta quan tâm đến các thay đổi liên tục của các yếu tố điều khiển (như nhiệt độ hoặc vị trí của các bức tường chứa chất khí) dẫn đến những thay đổi rời rạc trong các tham số vĩ mô. Những thay đổi này được gọi là chuyển pha (phase transitions).

Năng lượng tự do là đối tượng trung tâm của nghiên cứu vì các đạo hàm của nó sinh ra những đại lượng mà chúng ta quan tâm (như entropy, nhiệt dung - heat capacity, và áp suất - pressure). Do đó, một chuyển pha tương ứng với một gián đoạn trong một trong các đạo hàm của năng lượng tự do.

Tương tự, trong thiết lập của suy luận Bayesian, năng lượng tự do cũng sinh ra các đại lượng mà chúng ta quan tâm, chẳng hạn như kỳ vọng mất mát suy rộng (expected generalization loss): $$ G_n = \mathbb{E} _{X _{n+1}}[F _{n+1}] - F_n. $$

Ngoại trừ rằng số mẫu \(n\) là rời rạc, thì đây thực chất chỉ là một đạo hàm (derivative). ⁸ 8. Do đó, thực chất \(n\) là một dạng “nghịch đảo nhiệt độ” (inverse temperature), giống như \(\beta\). Việc tăng số lượng mẫu làm giảm nhiệt độ hiệu quả và đưa chúng ta tiến gần hơn đến trạng thái cơ bản (degenerate ground state).

Tương tự như trong học máy, chúng ta quan tâm đến việc làm thế nào các thay đổi liên tục trong mô hình hoặc trong phân phối đúng để dẫn đến các thay đổi rời rạc trong các hàm mà chúng ta triển khai và do đó gây ra sự gián đoạn trong năng lượng tự do và các đạo hàm của nó.

Một cách để kiểm tra câu hỏi này là nghiên cứu cách các mô hình thay đổi khi chúng ta giới hạn chúng trong một tập con của không gian tham số, \(\mathcal{W}^{(i)} \subset \mathcal{W}\). Điều gì xảy ra khi chúng ta thay đổi tập con này?

Nhắc lại rằng năng lượng tự do được định nghĩa như negative log của hàm phân hoạch. Khi ta giới hạn về \(\mathcal{W}^{(i)}\), ta thu được một năng lượng tự bị giới hạn (restricted free energy), $$ F_n(\mathcal{W}^{(i)}) := -\log Z_n(\mathcal{W}^{(i)}) = -\log \int_{\mathcal{W}^{(i)} \subset \mathcal{W}} \varphi(w)e^{-n\beta L_n(w)}dw = n\beta S_n(\mathcal{W}^{(i)}) + \lambda^{(i)}\log n - (m^{(i)} - 1)\log\log n + F^R(\xi) + o_p(1), $$

có dạng tiệm cận hoàn toàn tương tự (sau khi hoán đổi các tích phân trên toàn bộ không gian trọng số chỉ với các tích phân trên tập hợp con này). Sự khác biệt quan trọng là RLCT trong phương trình này là RLCT liên quan đến điểm kỳ dị lớn nhất trong \(\mathcal{W}^{(i)}\) chứ không phải điểm kỳ dị lớn nhất trong \(\mathcal{W}\).

Những gì chúng ta thấy là các chuyển pha trong quá trình học tương ứng với những thay đổi rời rạc trong hình học của cảnh quan mất mát “địa phương (local)” (tức là bị giới hạn, restricted). Hành vi kỳ vọng (expected behavior) của các mô hình trong những tập hợp này được quyết định bởi các điểm kỳ dị lớn nhất gần đó.

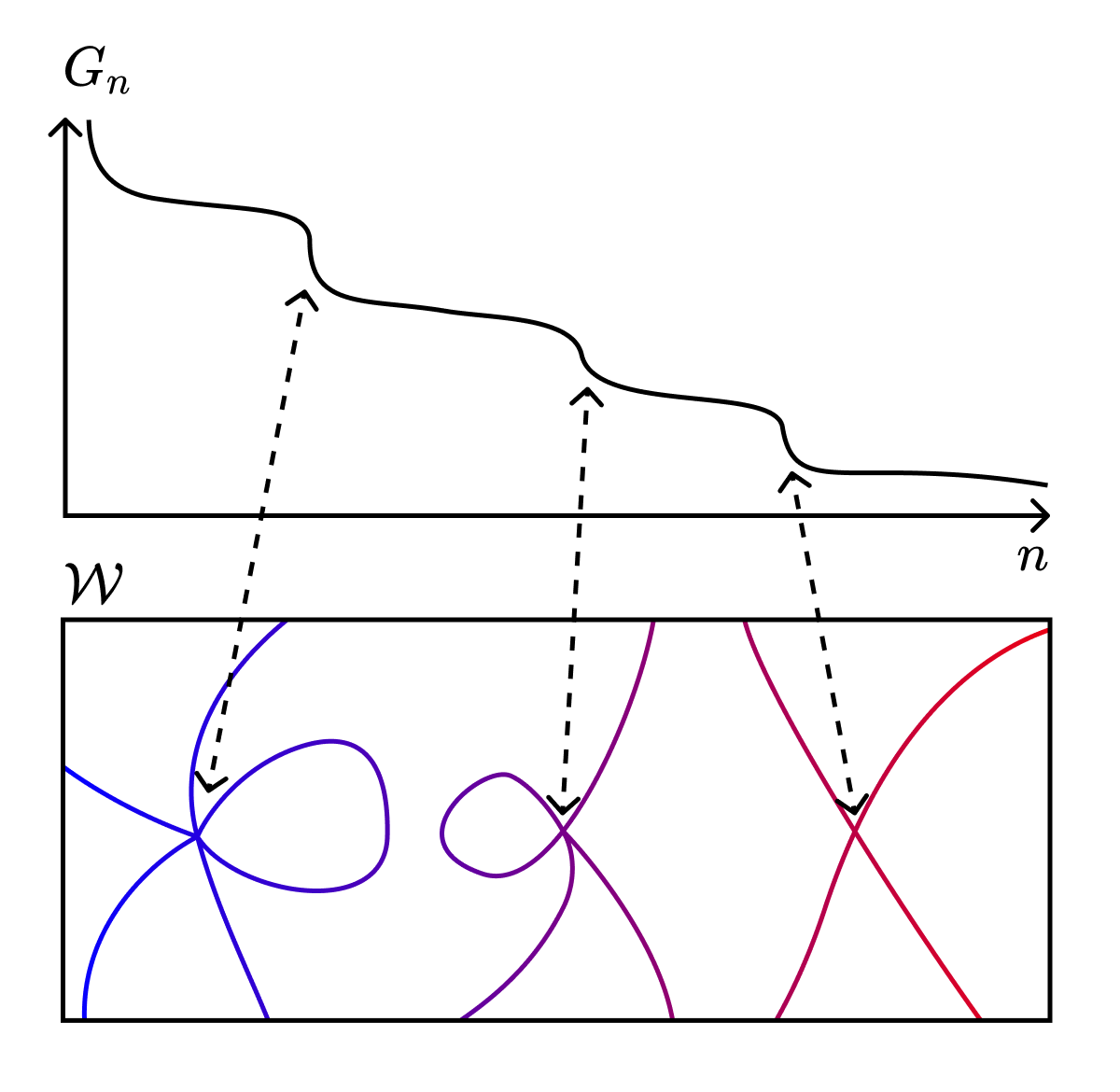
Nhìn từ góc độ này, mối liên hệ với Vật lý không chỉ là sự tự tin quá mức của các nhà vật lý khi áp đặt quan điểm của họ lên các lĩnh vực khác. Mối liên hệ này sâu sắc hơn nhiều.

Các nhà vật lý đã biết trong nhiều thập kỷ rằng hành vi vĩ mô của các hệ mà chúng ta quan tâm là hệ quả của các điểm tới hạn trong cảnh quan năng lượng: hành vi toàn cục bị chi phối bởi hành vi cục bộ của một tập hợp nhỏ các điểm kỳ dị. Điều này đúng ở khắp nơi, từ statistical physics, condensed matter theory, cho đến string theory.

Lý thuyết Học kỳ dị cho chúng ta thấy rằng các máy học không khác gì: hình học của các điểm kỳ dị là yếu tố cơ bản trong động lực học của việc học và khái quát hóa.

VI. Mạng neural là sự kỳ dị của tính đối xứng

Thủ thuật đẳng sau lý do mà mạng neural suy rộng tốt như thế là một số thứ giống như khả năng năng của chúng để khai phá tính đối xứng. Nhiều mô hình sử dụng ưu thế của parameter-function map không phải là một đơn ánh. Và với các mạng neural thì điều này được đưa lên một tầm cao mới.

Có các đối xứng hoán vị rời rạc, trong đó ta có thể lật hai cột trong một lớp miễn là ta lật hai hàng tương ứng trong lớp tiếp theo, ví dụ: $$ \begin{pmatrix} \textcolor{red}{a} & \textcolor{blue}{b} & c \\ \textcolor{red}{d} & \textcolor{blue}{e} & f \\ \textcolor{red}{g} & \textcolor{blue}{h} & i \end{pmatrix} \cdot \begin{pmatrix} \textcolor{red}{j} & \textcolor{red}{k} & \textcolor{red}{l} \\ \textcolor{blue}{m} & \textcolor{blue}{n} & \textcolor{blue}{o} \\ p & q & r \end{pmatrix} = \begin{pmatrix} \textcolor{blue}{b} & \textcolor{red}{a} & c \\ \textcolor{blue}{e} & \textcolor{red}{d} & f \\ \textcolor{blue}{h} & \textcolor{red}{g} & i \end{pmatrix} \cdot \begin{pmatrix} \textcolor{blue}{m} & \textcolor{blue}{n} & \textcolor{blue}{o} \\ \textcolor{red}{j} & \textcolor{red}{k} & \textcolor{red}{l} \\ p & q & r \end{pmatrix} $$

Có những đối xứng tỷ lệ liên quan đến hàm kích hoạt ReLU, $$ \text{ReLU}(x) = \frac{1}{\alpha}(\alpha x), \quad \alpha > 0, $$ và liên hệ với layer norm, $$ \text{LayerNorm}(\alpha x) = \text{LayerNorm}(x), \quad \alpha > 0, $$

(Lưu ý: Những điều này thường bị phá vỡ bởi sự hiện diện của regularization.)

Và có một đối xứng \(GL_n\) liên quan đến dòng dư thừa (ta có thể nhân ma trận embedding với bất kỳ ma trận khả nghịch nào miễn là ta áp dụng nghịch đảo của ma trận đó trước các khối attention, các lớp MLP, và lớp unembedding, và nếu ta áp dụng ma trận sau mỗi khối attention và lớp MLP).

Nhưng những đối xứng này thực ra không quá thú vị. Đó là vì chúng mang tính chất chung (generic). Chúng luôn tồn tại với bất kỳ lựa chọn \(w\) nào. Những đối xứng thú vị hơn là những đối xứng không tổng quát (non-generic symmetries) phụ thuộc vào \(w\).

Sự thay đổi trong các đối xứng không tổng quát này tương ứng với các chuyển pha trong xác suất hậu nghiệm; đây là cơ chế giúp các mạng neural thay đổi chiều hiệu dụng của chúng.

Các đối xứng không tổng quát này bao gồm những thứ như đối xứng nút suy biến (degenerate node symmetry) - là một trường hợp phổ biến khi một trọng số bằng không và không thực hiện được bất cứ công việc nào, và đối xứng tiêu diệt trọng số (weight annihilation symmetry) khi nhiều trọng số không bằng không nhưng kết hợp lại có hiệu quả trọng số bằng không.

Hệ quả là, ngay cả khi các bộ tối ưu hóa của chúng ta không thực hiện suy luận Bayesian một cách rõ ràng, những đối xứng không tổng quát này cho phép các bộ tối ưu hóa thực hiện một dạng lựa chọn mô hình nội tại. Có một sự đánh đổi giữa chiều hiệu dụng (effective dimensionality) thấp hơn và độ chính xác cao hơn, chịu ảnh hưởng bởi các loại chuyển pha giống như đã được thảo luận trong phần trước.

Động lực học có thể không hoàn toàn giống nhau, nhưng chính các điểm kỳ dị và các bất biến hình học của bề mặt mất mát (loss landscape) quyết định động lực học này.

VII. Thảo luận và các giới hạn hiện nay (Ý kiến về các phản bác của tác giả)

Tất cả các thảo luận trước đó đều áp dụng chung cho bất kỳ mô hình nào mà parameter-function mapping không phải là đơn ánh. Khi điều này xảy ra, Lý thuyết Học kỳ dị (SLT) không chỉ là một loạt giả thuyết thú vị và đáng tranh luận mà còn là một khung lý thuyết cần thiết.

Câu hỏi quan trọng hơn là liệu lý thuyết này có thực sự mang lại điều gì hữu ích trong thực tế hay không. Các đại lượng như RLCT cực kỳ khó tính toán cho các hệ thống thực tế, vậy chúng ta có thể thực sự áp dụng lý thuyết này không?

Tôi cho rằng câu trả lời là có, dù còn dè dặt. Các kết quả hiện tại cho thấy các dự đoán của SLT phù hợp với các thí nghiệm thực tế — các chuyển pha được dự đoán thực sự có thể quan sát được/ observable trong các toy models.

Điều đó không có nghĩa là không có những hạn chế. Tôi sẽ liệt kê một số từ nguồn này [3] và một số ý kiến riêng của tôi.

Trước khi đi sâu vào những phản biện thực sự của tôi, sau đây là một số phản biện mà tôi cho là không thực sự tốt:

• “Nhưng chúng ta quan tâm đến việc xấp xỉ hàm!”: Thảo luận này diễn ra trong một bối cảnh rất xác suất. Trong thực tế, chúng ta đang làm việc với các hàm mất mát và xấp xỉ hàm, không phải mật độ. Tôi không nghĩ đây là vấn đề lớn vì thông thường có thể khôi phục cơ sở Bayesian của bạn ngay cả trong việc xấp xỉ hàm xác định. Ngay cả khi không làm được điều đó, tuyên bố chung — rằng hình học của các điểm kỳ dị quyết định động lực học — dường như vẫn khá vững chắc.

• “Nhưng chúng ta không huấn luyện đến hoàn chỉnh!”: Tôi mong đợi hầu hết các kết quả sẽ đúng với bất kỳ tập mức mất mát nào — chúng ta chỉ quan tâm đến các điểm kỳ dị nổi trội trong các tập mức mà chúng ta đạt được (ngay cả khi chúng không tối thiểu hóa mất mát hoàn hảo).

• “Nhưng việc tính toán (và thậm chí xấp xỉ) RLCT là không khả thi.”: Việc biết sự tồn tại lý thuyết của một thứ có thể giúp ích trong những trường hợp ban đầu tưởng chừng không liên quan. Một phản biện lạc quan hơn là: “Có thể chúng ta tính được điều này cho các mạng neural đơn lớp đơn giản, rồi tìm cách mở rộng lặp đến các lớp sâu hơn.” Điều này thực sự không quá vô lý.

• “Nhưng làm sao chuyển đổi kết quả từ \(\tanh\) sang các hàm kích hoạt thực tế như swish?”: Giống như nhiều định lý xấp xỉ phổ quát (universal approximation theorems) không phụ thuộc vào chi tiết của hàm kích hoạt, tôi không nghĩ đây là một phản biện lớn đối với lý thuyết.

• “Nhưng mạng ReLU không phải có tính giải tích.”: Tôi không rõ, nhưng dường như điều này không quan trọng.

• “Nhưng các giới hạn tiệm cận ở \(n\) thực sự nói gì về trường hợp hữu hạn?”: Theo quan điểm của tôi trong vật lý thống kê, vài nghìn tỷ mẫu dữ liệu gần với vô hạn hơn là về không.

• “Nhưng tất cả điều này chỉ là cách diễn đạt phức tạp của ý tưởng rằng các bể rộng chi phối toàn bộ?”: Thực tế, câu hỏi mà SLT trả lời dường như là một câu hỏi khác: nó nói về lý do tại sao chúng ta kỳ vọng các mô hình nói chung (và dựa trên các khoảnh khắc bậc cao hơn) có thể khái quát hóa.

Những phản biện thực sự của tôi như sau:

• “Nhưng các dự đoán về ’lỗi khái quát hóa’ thực chất là một thiết bị lý thuyết không liên quan đến ’lỗi khái quát hóa’ mà chúng ta hiểu trong ML.”: Đây là một ý kiến hợp lý, nhưng tôi lạc quan rằng chúng ta có thể tìm ra các đại lượng mà chúng ta thực sự quan tâm từ những gì hiện tại chúng ta tính được.

• “Nhưng suy luận Bayesian liên quan gì đến SGD và các biến thể của nó?”: Điều này quan trọng, đặc biệt khi tôi không hoàn toàn tin vào quan điểm rằng các mạng neural đang thực hiện suy luận Bayesian. Đây vẫn là nguồn nghi ngờ lớn nhất của tôi.

• “Nhưng phân phối thực sự không khả kiến.”: Trong phần trình bày này, chúng ta giả định rằng có một lựa chọn tham số \(w_0\) sao cho \(p(x \mid w_0)\) bằng \(q(x)\) gần như ở khắp mọi nơi (đây là tính “khả kiến” hay “hạt nhân sự thật”). Ở các hệ thống thực tế, điều này không bao giờ đúng. Đối với các lý thuyết có thể chuẩn hóa (renormalizable) ¹⁰ 10. Renormalizable: Một từ có ý nghĩa kỹ thuật cụ thể nhưng liên quan đến chuẩn hóa trong vật lý thống kê. , việc mở rộng kết quả sang trường hợp không thể thực hiện được hóa ra không quá khó. Đối với các lý thuyết không thể chuẩn hóa (non-renormalizable), chúng ta đang ở trong một miền đất mới lạ.

VIII. Chúng ta sẽ đi đến đâu? (Ý kiến định hướng tương lai của tác giả)

Hy vọng rằng bạn đã cảm nhận được những điểm đặc sắc từ Lý thuyết Học kỳ dị (Singular Learning Theory) và những góc nhìn mà nó mang lại: cảm giác rằng Lý thuyết Học giống như Vật lý kết hợp với xác suất triển vọng, rằng Học là nhiệt động lực học của mất mát (thermodynamics of loss), rằng khái quát hóa/ tổng quát hóa/ khả năng suy rộng là sự hiện diện của kỳ dị và mối quan hệ sâu sắc mang tính phổ quát giữa hành vi toàn cục và hình học địa phương của các điểm kỳ dị.

Công việc này còn rất xa mới hoàn thành, nhưng tác động tiềm năng của nó đến sự hiểu biết của chúng ta về trí tuệ là sâu sắc.

Để kết thúc, hãy cùng khám phá một hướng đi mà tôi thấy đặc biệt thú vị — lý thuyết học kỳ dị như một con đường để dự đoán các quy luật mở rộng (scaling laws) mà chúng ta quan sát được trong các mô hình học sâu [5].

Có sự suy đoán rằng chúng ta có thể chuyển giao các công cụ và ý tưởng của nhóm tái chuẩn hóa (renormalization group), một tập hợp kỹ thuật được phát triển trong vật lý để xử lý các hiện tượng tới hạn và quy mô, nhằm hiểu các chuyển pha (phase transitions)trong các máy học, và cuối cùng là tính toán các hệ số mở rộng từ các nguyên lý đầu tiên.

Mượn lời kêu gọi hành động của Dan Murfet (call to arms) [3]:

It is truly remarkable that resolution of singularities, one of the deepest results in algebraic geometry, together with the theory of critical phenomena and the renormalisation group, some of the deepest ideas in physics, are both implicated in the emerging mathematical theory of deep learning. This is perhaps a hint of the fundamental structure of intelligence, both artificial and natural. There is much to be done!

Thật đáng kinh ngạc khi việc giải quyết các điểm kỳ dị, một trong những kết quả sâu sắc nhất của hình học đại số, cùng với lý thuyết về hiện tượng tới hạn và nhóm tái chuẩn hóa, một số ý tưởng sâu sắc nhất trong vật lý, đều có liên quan đến lý thuyết toán học đang nổi lên của học sâu. Đây có lẽ là một gợi ý về cấu trúc cơ bản của trí tuệ, cả nhân tạo lẫn tự nhiên. Còn rất nhiều việc phải làm!

IX. Tài liệu tham khảo

[1]: Watanabe 2009

[2]: Carroll 2021

[3]: Metauni 2021-2023 (Super awesome online lecture series hosted in Roblox that you should all check out.)

[4]: Guedj 2019

[5]: Kaplan 2020