Các thuật toán dự đoán liên kết

Nov. 3, 2023

Mở đầu

Dịch từ: Link prediction algorithms

"Prediction is very difficult, especially if it's about the future." (Tạm dịch: Dự đoán thì rất là khó, đặc biệt là khi nói về tương lai!.) —Nils Bohr, Nobel laureate in Physics


Mạng xã hội (social networks) là một cách phổ thông để mô hình tương tác giữa con người trong một nhóm hay cộng đồng. Chúng có thể được trực quan hóa như đồ thị (graphs), trong đó một đỉnh (vertex) tương ứng với một người trong một số nhóm và một cạnh thể hiện một số dạng của sự liên hệ giữa những người tương ứng. Mạng xã hội luôn luôn động (dynamic) vì những cạnh mới và những đỉnh mới được thêm vào đồ thị theo thời gian. Hiểu về tính động, tức là sự phát triển của một mạng xã hội là một bài toán phức tạp do ta phải xử lý một số lượng lớn các biến tham số (variable parameters).

Nhưng, một bài toán tương đối dễ hơn là hiểu về mối liên kết giữa hai nút cụ thể. Ví dụ như, một số câu hỏi thú vị mà có thể được đưa ra như sau:

Trong thực tế, bài toán dự đoán liên kết yêu cầu: sự phát triển của mạng xã hội có thể được mô hình hóa ở mức độ nào bằng cách sử dụng các đặc trưng nội tại của cấu trúc tô-pô mạng? Trạng thái hiện tại của mạng có thể được sử dụng để dự đoán các liên kết trong tương lai không?

Bài toán dự đoán liên kết cũng được liên hệ với bài toán suy diễn các liên kết bị thiếu (problem of inferring missing links) từ một mạng quan sát được: trong một số miền tri thức, người ta xây dựng một mạng lưới của sự tương tác dựa trên dữ liệu quan sát được, và sau đó cố gắng suy diễn những liên kết bổ sung mà không xuất hiện trực tiếp và có khả năng tồn tại. Vấn đề khác với bài toán dự đoán liên kết ở chỗ nó thực thi với một đồ thị tĩnh (một snapshot), thay vì xem xét sự phát triển của mạng; nó cũng có xu hướng tính đến các thuộc tính cụ thể của các nút trong mạng, thay vì đánh giá sức mạnh của các phương pháp dự đoán hoàn toàn dựa trên cấu trúc đồ thị.[2]

Ví dụ, trong trường hợp của facebook, với tính năng “friend finder”, họ có thể đề xuất những người mà bạn thấy đủ thú vị để kết nối có thể dẫn đến tình bạn thực sự ngoài đời thực (người giới thiệu bạn mới), điều này có thể nâng cao lòng trung thành của cả hai bên đối với dịch vụ của facebook (do đó giúp facebook kiếm được nhiều tiền hơn). Hoặc họ có thể gợi ý những người bạn mà bạn đã biết nhưng chưa kết nối qua facebook (xây dựng mạng lưới tình bạn hiện tại trên facebook). Ví dụ sau tương ứng với phát biểu của vấn đề ban đầu trong khi ví dụ trước tương ứng với dự đoán về các liên kết bị thiếu (vấn đề liên quan thứ hai). Thật vậy, facebook chỉ cố gắng thực hiện nhiệm vụ thứ hai.

Vượt ra ngoài ngữ cảnh mạng xã hội, bài toán dự đoán liên kết có nhiều ứng dụng khác. Ví dụ, trong sinh tin học (bioinformatics), dự đoán liên kết có thể được sử dụng để tìm tương tác giữa các protein; trong kinh tế số (e-commerce), nó có thể giúp ích trong việc xây dựng các hệ thống gợi ý như tính năng “people who bought this also bought” trên Amazon; và trong lĩnh vực bảo mật (security domain), dự đoán liên kết có thể hỗ trợ trong việc xác định các nhóm ẩn danh của những kẻ khủng bố hoặc tội phạm. Hơn nữa, nhiều nghiên cứu được tiến hành trên mạng đồng tác giả (co-authorship networks) (ví dụ như trong các tạp chí khoa học, với các cạnh nối các cặp có bài báo đồng tác giả). Hai nhà khoa học “thân thiết” trong mạng lưới sẽ có những đồng nghiệp chung và sẽ đi theo những vòng tròn tương tự nhau; sự gần gũi về mặt xã hội này cho thấy rằng bản thân họ có nhiều khả năng cộng tác hơn trong tương lai gần. Do đó, dự đoán liên kết trong ứng dụng này có thể được sử dụng để tăng tốc kết nối/hợp tác chuyên môn hoặc học thuật cùng có lợi mà lẽ ra sẽ mất nhiều thời gian hơn để hình thành một cách tình cờ.

Phát biểu bài toán

Cho trước một đồ thị vô hướng, không trọng số (unweighted, undirected graph), $G = (V, E)$ thể hiện cấu trúc tô-pô của một mạng xã hội mà trong đó mỗi cạnh $e = \left \langle u,v\right \rangle \in E$ thể hiện một tương tác giữa $u$ và $v$ xuất hiện ở một thời gian cụ ghể $t(e)$.


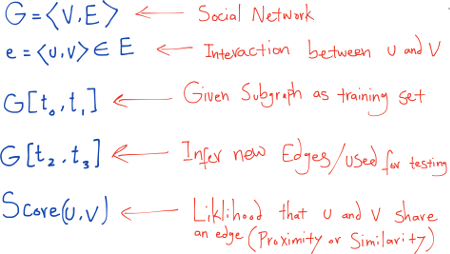
Và cũng, với một nút $x$, $\Gamma(x)$ thể hiện tập các láng giềng của $x$. $Degree(x)$ là kích thước của $\Gamma(x)$.

Với hai thời điểm, $t$ và $t’ > t$, gọi $G[t,t’]$ đại diện cho đồ thị con của $G$ bao gồm tất cả các cạnh với một khoảng thời gian giữa $t$ và $t’$. Gọi $t_0$, $t’_0$, và $t’_1$ là bốn thời điểm, trong đó $t_0 < t’_0 \leq t_1 < t’_1$. Ta có bài toán dự đoán liên kết:


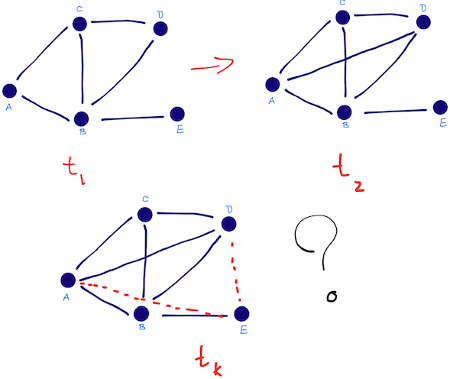
Cho trước một snapshot của mạng xã hội tại thời điểm $t$ (hoặc sự phát triển mạng giữa $t_1$ và $t_2$), tìm cách dự đoán chính xác các cạnh sẽ được thêm vào mạng trong khoảng thời gian từ thời gian $t$ (hoặc $t_2$) đến thời điểm $t'$ nhất định trong tương lai.

Để sinh ra danh sách này, chúng ta sử dụng các thuật toán heuristic (heuristic algorithms) mà gán một ma trận tương đồng (similarity matrix) $S$ mà những phần tử thực $s_{xy}$ là điểm số giữa $x$ và $y$. Điểm này có thể được xem như thước đo mức độ tương đồng giữa các nút $x$ và $y$. Với mỗi cặp nút, $x, y \in V$, một cách tổng quát $s_{xy} = s_{yx}$. Tất cả các liên kết không tồn tại được sắp xếp theo thứ tự giảm dần theo điểm số của chúng và các liên kết ở trên cùng có nhiều khả năng tồn tại nhất. [4]

Vì chúng ta thực sự không thể dự đoán tương lai nên để kiểm tra độ chính xác của thuật toán, một phần liên kết được quan sát $E$ (giả sử là $90%$ tổng số) của một số tập dữ liệu tương tác đã biết được chọn ngẫu nhiên dưới dạng tập huấn luyện, $ET$, phần còn lại các liên kết (10% tổng số) được sử dụng làm bộ thăm dò, $EP$, để dự đoán và không có thông tin nào trong bộ này được phép sử dụng để dự đoán. Một cách rõ ràng, $E = ET \cup EP$ và $ET \cap EP = \oslash$. Chất lượng dự đoán được đánh giá bằng một độ đo tiêu chuẩn (standard metric), diện tích dưới đường cong ROC (AUC - Area under the ROC Curve). Số liệu này có thể được hiểu là xác suất liên kết bị thiếu được chọn ngẫu nhiên (liên kết trong $EP$) được cho điểm cao hơn liên kết không tồn tại được chọn ngẫu nhiên (liên kết trong $U$ nhưng không phải trong $E$, trong đó $U$ biểu thị tập phổ quát) [8]. Trong số $n$ so sánh độc lập, nếu có $n’$ lần xuất hiện liên kết bị thiếu có điểm cao hơn và $n’’$ lần xuất hiện liên kết bị thiếu và liên kết không tồn tại có cùng điểm, chúng tôi xác định độ chính xác là:

$$ AUC = \frac{n’ + 0.5n’’}{n} $$

Nếu tất cả các điểm được tạo ra từ một phân phối độc lập và giống hệt nhau thì độ chính xác sẽ vào khoảng 0,5. Do đó, mức độ chính xác vượt quá 0,5 cho thấy thuật toán hoạt động tốt hơn bao nhiêu so với cơ hội thuần túy.


Những lối tắt hữu dụng

Các mạng xã hội được định nghĩa bởi các cấu trúc mà nút của nó thể hiện con người hoặc những thực thể khác được nhúng trong một ngữ cảnh xã hội, và những cạnh của nó thể hiện tương tác, cộng tác, hoặc tác động giữa những thực thể. Như vậy, những mạng lưới này có nhiều thuộc tính thường được biết, như power law degree distribution [Barabasi and Albert 1999], small world phenomenon [Watts and Strogatz 1998], community structure (clustering effect) [Girvan and Newman 2002].

Tác động thế giới nhỏ - small world effect chỉ đến hiện tượng mà trung bình khoảng cách trong mạng lưới thì rất nhỏ để so sánh với kích thước của mạng. Điều đó có nghĩa là mỗi cặp nút có thể được kết nối thông qua một đường dẫn ngắn trong mạng. Trong thí nghiệm nổi tiếng của mình, Stanley Milgram đã thách thức mọi người gửi bưu thiếp đến một người nhận cố định bằng cách chỉ chuyển chúng qua những người quen biết trực tiếp. Milgram phát hiện ra rằng số lượng trung gian trung bình trên đường đi của bưu thiếp nằm trong khoảng từ 4,4 đến 5,7, tùy thuộc vào mẫu người được chọn. Facebook vừa mới báo cáo kết quả tính toán khoảng cách đồ thị mạng xã hội quy mô thế giới (world-scale social-network graph-distance computation) đầu tiên của họ, sử dụng toàn bộ mạng lưới người dùng đang hoạt động của Facebook (721 triệu người dùng, 69 tỷ liên kết bạn bè). Họ phát hiện ra rằng khoảng cách trung bình là 4,74, tương ứng với 3,74 trung gian hay “degrees of separation - bậc tách biệt”.


Small world effect

Tác động phi quy mô - scale-free effect chỉ đến hiện tượng mà hầu hết các liên kết của các nút thì rất nhỏ trong mạng lưới; chỉ một số ít nút có nhiều liên kết. Trong mạng lưới như thế, các nút với bậc cao được gọi là hubs (hinge node). Nút hub thống trị sự vận hành của mạng lưới. Tác động phi quy mô hay scale-free effect cho thấy phân phối bậc nút không đồng đều một cách nghiêm trọng trong mạng quy mô lớn (areto, heavy-tailed, or Zipfian degree distributions). Hiện tượng này được ghi nhận ở mức độ phân bổ của mạng toàn cầu (world-wide web).


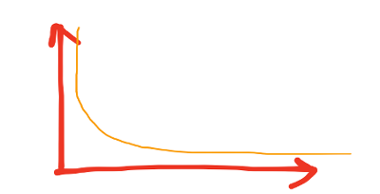
Power law degree distribution

Tác động gom cụm - clustering effect đề cập đến hiện tượng có một nhóm bạn bè, người quen, vòng tròn và các nhóm nhỏ khác trên mạng xã hội. Mỗi thành viên trong nhóm nhỏ đều biết nhau. Hiện tượng này cũng có thể được mô tả bằng khái niệm đóng cửa bộ ba: có nhiều sơ đồ con được kết nối đầy đủ trong mạng xã hội.

Tại sao đây là một bài toán khó

Với một mạng xã hội $G(V, E)$, ở đây có $V \times V - E$ cạnh khả thi để lựa chọn, nếu chúng ta chọn một cách ngẫu nhiên một cạnh để dự đoán cho mạng xã hội đang tồn tại của chúng ta. Nếu $G$ dày đặc, thì $E \approx V^2 - b$ trong đó $b$ là một hằng số giữa $1$ và $V$. Dẫn đến, ta có một số lượng cạnh cố định để chọn, và $O(1/c)$ xác suất của việc chọn đúng đắn một cách ngẫu nhiên. Nếu $G$ thưa, thì $E \approx V$. Dẫn đến, ta có $V^2$ cạnh để chọn, và $O(1/V^2)$ xác suất của việc chọn đúng một cách ngẫu nhiên. Không may rằng các mạng xã hội thường là các mạng thưa, và do đó việc chọn một cách ngẫu nhiên là một ý tưởng tệ!

Trong bộ dữ liệu DBLP, vào năm 2000. tỷ lệ liên kết thực sự và khả thi là rất thấp, $2 \times 10^{-5}$. Vì vậy, trong một tập dữ liệu được lấy mẫu thống nhất với một triệu trường hợp huấn luyện, chúng ta chỉ có thể mong đợi 20 trường hợp tích cực. Tệ hơn nữa, tỷ lệ giữa số lượng liên kết tích cực và số lượng liên kết có thể có cũng giảm dần theo thời gian, vì các liên kết tiêu cực tăng trưởng bậc hai trong khi liên kết tích cực chỉ tăng trưởng tuyến tính với một nút mới.

Trong khoảng thời gian 10 năm, từ 1995 đến 2004, số lượng tác giả trong DBLP đã tăng từ 22 nghìn lên 286 nghìn, nghĩa là số lượng hợp tác có thể tăng lên theo hệ số 169, trong khi số lượng hợp tác thực tế chỉ tăng theo hệ số 21.

Những khoảng cách tương đồng

Graph Distance - Khoảng cách đồ thị

Có lẽ khoảng cách trực tiếp để định lượng hai nút tương đồng như thế nào là khoảng cách đồ thị (graph distance). Nó được định nghĩa bằng âm khoảng cách đường đi ngắn nhất (negative of the shortest-path distance) từ $x$ đến $y$.

Lưu ý rằng, khi đồ thị $G$ có hàng triệu đỉnh, thật không hiệu quả nếu áp dụng thuật toán $Dijkstra$ để tính toán khoảng cách đường đi ngắn nhất từ $x$ đến $y$. Thay vì vậy, ta khai phá tính chất thế giới nhỏ (small-world) của mạng xã hội và áp dụng vòng tìm kiếm được mở rộng để tính toán khoảng cách đường đi ngắn nhất từ $x$ đến $y$.


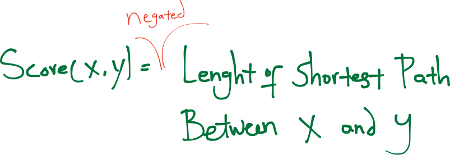
Độ đo này tuân theo quan điểm cho rằng mạng xã hội là những thế giới nhỏ (small world), trong đó các cá thể (individuals) có liên quan với nhau thông qua các mắt xích ngắn.

Một cách cụ thể, ta khởi tạo tập $S = \{x\}$ và $D = \{y\}$. Trong mỗi bước, ta mở rộng tập $S$ để bao gồm những thành phần láng giềng của nó, tức là $S = S \cup \{v \mid \left \langle u, v \right \rangle \in E \wedge u \in S\}$, hoặc mở rộng tập $D$ để bao gồm những thành phần không là láng giềng của nó, tức là $D = D \cap \{v \mid \left \langle u, v \right \rangle \in E \wedge v \in D\}$. Ta dừng thuật toán khi $S \cap D \ne \oslash$. Số bước đã thực hiện cho đến hiện tại cho ta khoảng cách đường đi ngắn nhất. Để hiệu quả, ta luôn luôn mở rộng tập nhỏ hơn giữa $S$ và $D$ trong mỗi bước. [10]


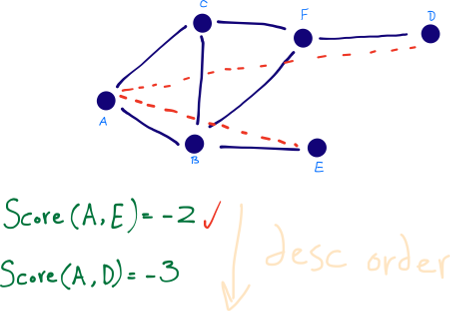
Việc sử dụng khoảng cách đường đi ngắn nhất bị phủ định (thay vì ban đầu) đảm bảo rằng độ gần $GD(x,y)$ tăng khi $x$ và $y$ tiến gần hơn.

Common Neighbors - Láng giềng chung

Láng giềng chung dựa trên quan niệm rằng hai người lạ có một người bạn chung có thể được người bạn đó giới thiệu. Quan niệm này có tác động của “tam giác đóng” trong đồ thị và giống như một cơ chế phần chung trong cuộc sống đời thật. Newman [7] đã tính toán định lượng này trong ngữ cảnh các mạng cộng tác (collaboration networks), xác định một tương quan dương giữa số lượng láng giềng chung của $x$ và $y$ tại thời điểm $t$, và xác suất mà $x$ và $y$ sẽ cộng tác tại một số thời điểm sau $t$.


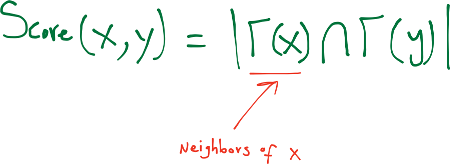
độ phức tạp của việc so sánh danh sách: $O(V \cdot VlogV)$


tam giác đóng

Jaccard’s Coefficient - Hệ số Jaccard

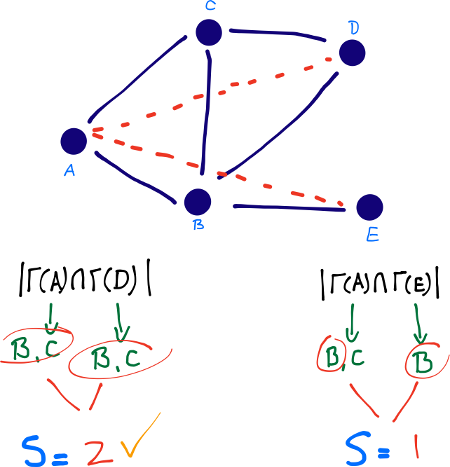
Hệ số Jaccard, một khoảng cách tương đồng (similarity metric) mà được sử dụng thường xuyên trong truy vấn thông tin (information retrieval), nó đo lường xác suất mà cả $x$ và $y$ có cùng đặc trưng $f$, với một cách ngẫu nhiên với đặc trưng được lựa chọn $f$ mà hoặc $x$ hoặc $y$ có. Nếu ta lấy “đặc trưng” ở đây trở thành các láng giềng, thì độ do9 này nắm bắt quan điểm hấp dẫn về trực giác rằng tỷ lệ các đồng tác giả của $x$ cũng đã từng làm việc với $y$ (và ngược lại) là một thước đo tốt về sự giống nhau của $x$ và $y$.


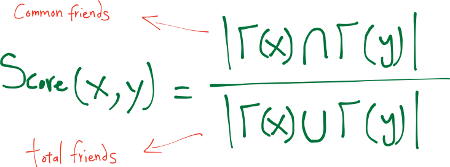
Khoảng cách này giải quyết vấn đề trong đó hai nút có thể có nhiều nút lân cận chung vì chúng có nhiều nút lân cận chứ không phải vì chúng có liên quan chặt chẽ với nhau.

Adamic/Adar (Frequency-Weighted Common Neighbors) - Tần số có trọng số láng giềng chung

Độ đo này tinh chỉnh việc đếm các đặc trưng chung đơn giản bằng cách đánh trọng số thể hiện mức độ quan trọng của đặc trưng. Bộ dự đoán Adamic/Adar thể hiện quan điểm các đặc trưng “hiếm” thì ẩn chứa nhiều thứ bên trong; những tài liệu có chung cụm từ “for example” thì có lẽ ít giống nhau hơn các tài liệu có chung cụm từ “clustering coefficient”.


độ phức tạp của việc so sánh danh sách: $O(V \cdot VlogV)$

Nếu “đóng tam giác” là một cơ chế tần xuất (frequent mechanism) theo đó các cạnh mới hình thành trong mạng xã hội, thì để $x$ và $y$ được giới thiệu bởi một người bạn chung $z$, người $z$ sẽ phải chọn giới thiệu cặp $⟨x,y$⟩ từ (chọn $|\Gamma(z)|$ với 2) cặp bạn bè của người ấy; do đó, một người không được ưa chuộng (người không có nhiều bạn bè) có thể có nhiều khả năng giới thiệu một cặp bạn bè cụ thể của mình với nhau hơn.


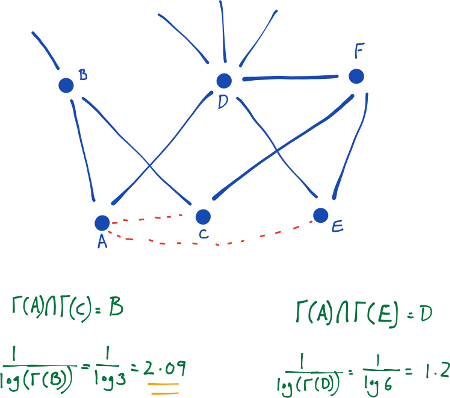
triadic closure

Preferential Attachment

Một khái niệm phổ biến trong lĩnh vực nghiên cứu mạng xã hội là những người dùng với nhiều bạn bè thường có xu hướng tạo ra nhiều mối liên kết hơn trong tương lai. Đó là vì theo những dữ kiện mà trong một số mạng xã hội, như trong kinh tế, người giàu thì càng giàu hơn.


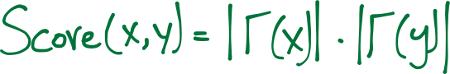
formal equation

Chúng ta ước tính mức độ “giàu” của hai đỉnh bằng cách tính toán phép nhân giữa số lượng bạn bè ($|\Gamma(x)|$) hoặc số người theo dõi mà mỗi đỉnh có. Có thể lưu ý rằng chỉ số tương đồng (similarity index) không yêu cầu bất kỳ thông tin nút lân cận nào; do đó, chỉ số tương tự này có độ phức tạp tính toán thấp nhất.


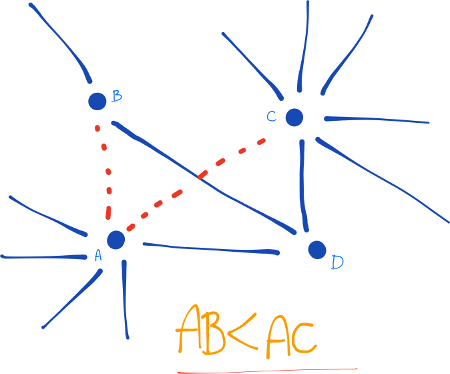
Liên kết giữa A và C có nhiều khả năng xảy ra hơn liên kết giữa A và B vì C có nhiều lân cận hơn B.

Katz (Exponentially Damped Path Counts - số lượng đường đi bị suy giảm theo cấp số nhân)

Heuristic này định nghĩa một độ đo mà tính tổng trực tiếp trên tập hợp các đường đi, giảm dần theo cấp số nhân bởi chiều dài để đếm các đường đi ngắn nhất. Độ đo Katz là một biến thể của độ đo đường đi ngắn nhất (shortest-path measure). Ý tưởng đằng sau độ đo Katz là càng có nhiều đường đi giữa hai đỉnh và những đường đi này càng ngắn thì kết nối càng mạnh.


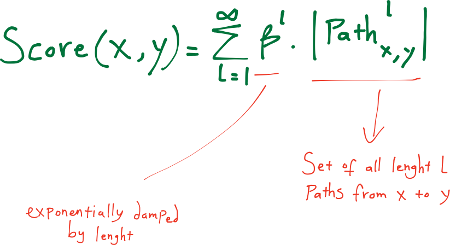
Một $\beta$ rất nhỏ mang lại những dự đoán giống như láng giềng chung, bởi vì các đường đi có độ dài bằng ba hoặc nhiều hơn đóng góp rất ít vào tổng.


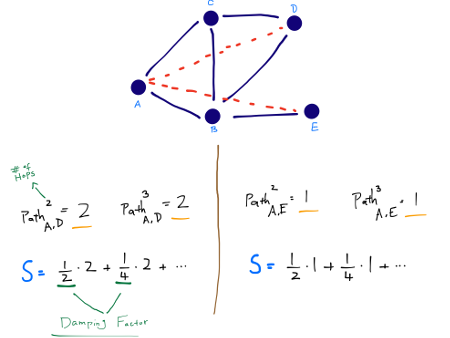
Hitting Time

Một bước đi ngẫu nhiên bắt đầu tại một nút $x$ và di chuyển tuần tự đến một lân cận ngẫu nhiên của $x$. Hitting time $H_{x, y}$ từ $x$ đến $y$ là kỳ vọng số lượng bước nhảy cần thiết để cho một bước đi ngẫu nhiên bắt đầu tại $x$ chạm đến $y$.


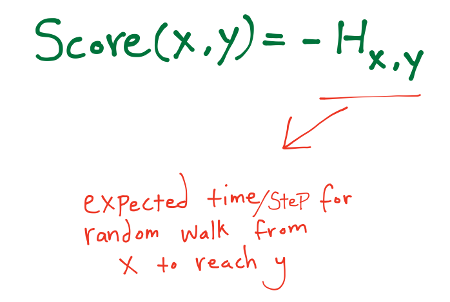
độ phức tạp của việc so sánh danh sách: $O(V \cdot VlogV)$

Một khó khăn khi sử dụng hitting time như một độ đo tương đồng là $H_{x, y}$ tương đối nhỏ với bất kỳ $y$ là một nút với xác suất dừng (stationary probability) $\pi y$ lớn, bất kể nút $x$ là nút nào. Nghĩa là, đối với nút $y$ mà tại đó bước đi ngẫu nhiên dành một lượng thời gian đáng kể trong giới hạn, thì bước đi ngẫu nhiên sẽ sớm đến $y$, hầu như bất kể nó bắt đầu ở đâu. Do đó, các dự đoán được đưa ra dựa trên $H_{x, y}$ có xu hướng chỉ bao gồm một vài nút riêng biệt $y$. Để giải quyết vấn đề này, người ta xem xét phiên bản chuẩn hóa của hitting và số lần tương tác bởi định nghĩa:

$$\text{score}(x, y) = -H_{x, y} \cdot \pi y$$

Rooted PageRank

Một khó khăn khác khi sử dụng các độ đo dựa trên thời gian đánh và thời gian tương tác là sự phụ thuộc nhạy cảm của chúng vào các phần của đồ thị ở xa từ $x$ và $y$, ngay cả khi $x$ và $y$ được kết nối bằng những đường đi rất ngắn. Một cách để giải quyết khó khăn này là cho phép bước đi ngẫu nhiên từ $x$ đến $y$ để “đặt lại” theo chu kỳ, quay trở lại $x$ với xác suất cố định $\alpha$ ở mỗi bước; bằng cách này, các phần ở xa của đồ thị sẽ hầu như không bao giờ được khám phá.


Việc đặt lại ngẫu nhiên tạo thành cơ sở của độ đo PageRank cho các trang web và chúng tôi có thể điều chỉnh nó để dự đoán liên kết. Các cách tiếp cận tương tự đã được xem xét đối với PageRank được cá nhân hóa (personalized PageRank), trong đó người ta muốn xếp hạng các trang web dựa trên cả “tầm quan trọng (importance)” tổng thể (cốt lõi của PageRank) và mức độ liên quan đến một chủ đề hoặc cá nhân cụ thể, bằng cách thiên về các lần đặt lại ngẫu nhiên đối với các trang có liên quan theo chủ đề hoặc được đánh dấu trang.

Các khoảng cách khác

Một độ đo khác có thể được sử dụng là độ đo Friends-measure. Khi xem xét hai đỉnh trong mạng xã hội, ta có thể giả định rằng các vùng lân cận của chúng càng có nhiều kết nối với nhau thì khả năng hai đỉnh được kết nối với nhau càng cao. Ta lấy logic của phát biểu và xác định thước đo Friends-measure là số lượng kết nối giữa các vùng lân cận $u$ và $v$. Ta có thể nhận thấy rằng trong các mạng vô hướng, thước đo Friends-measure là trường hợp riêng của thước đo Katz trong đó $\beta = 1$ và $I_{max} = 2$.


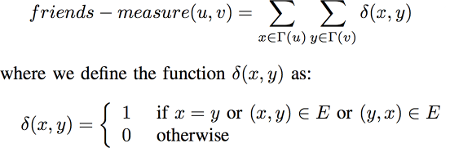
Một số kết quả thực nghiệm

Trong số này, các thuật toán dựa trên nút lân cận có khả năng mở rộng hạn chế và không nhất thiết tạo thành một cách tiếp cận khả thi cho các mạng User Generated Content networks [9]. Ví dụ: Facebook có hơn một tỷ người dùng đã đăng ký và mỗi tháng có nhiều người dùng mới được thêm vào. Hơn nữa, sự phân bổ mức độ quy luật lũy thừa trong mạng xã hội cho thấy rằng có một số cá nhân có số lượng kết nối (trung tâm) lớn. Việc tính toán các đặc điểm tôpô cục bộ trên một sơ đồ con chỉ bao gồm bạn bè của những cá nhân này có thể cần nhiều tính toán.

Dưới đây là các biểu đồ hiệu suất được tính toán bởi Liben-Nowell và Kleinberg vào năm 2003, người đã nghiên cứu tính hữu ích của các đặc điểm tôpô đồ thị bằng cách kiểm tra chúng trên năm bộ dữ liệu mạng đồng tác giả, mỗi bộ chứa hàng nghìn tác giả [3].


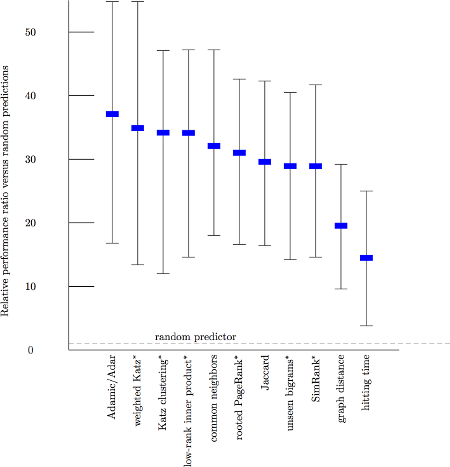
Con số bên trái là số yếu tố cải thiện so với dự đoán ngẫu nhiên. tức là độ đo Adamic/Adar chính xác hơn khoảng 37 lần so với độ đo ngẫu nhiên.


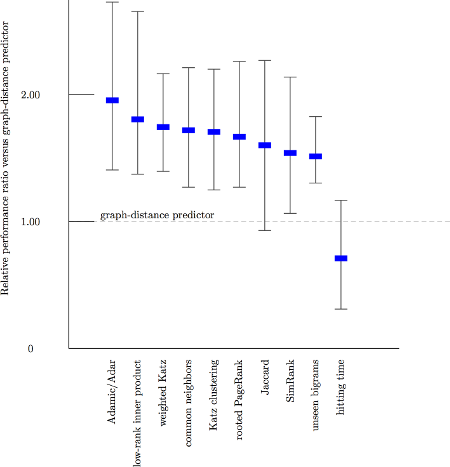
So sánh với công cụ dự đoán khoảng cách biểu đồ làm đường cơ sở. Những cải tiến đột ngột có vẻ không ấn tượng lắm.


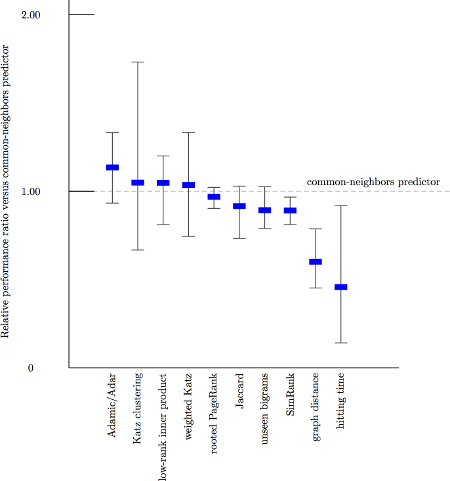
So sánh với yếu tố dự đoán hàng xóm chung làm đường cơ sở. Các biện pháp khác bây giờ chỉ tốt hơn một chút!


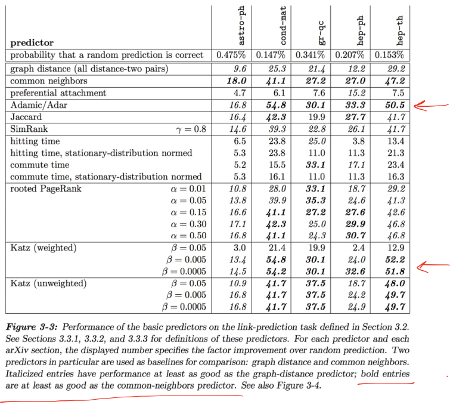
Biểu đồ hiển thị kết quả bằng số trên nhiều phần của mạng đồng tác giả arVix. Các phần khác nhau của arXiv mang lại kết quả khác nhau.

Các phương pháp tiếp cận khác

Mặc dù các đặc trưng nội tại (features intrinsic) của một mạng lưới có thể cung cấp một độ đo tốt để chỉ rằng khả năng liên kết trong tương lai, có nhiều phương pháp/ độ đo khác cũng được đề xuất mà sử dụng một biến thể của những heuristic được đề cập. Lấy ví dụ, các đặc trưng Extra-network có thể cải thiện đáng kể độ chính xác của dự đoán (tức là những từ hóa mô tả sự quan tâm của mỗi nhà khoa học, hay những từ khóa được rút trích từ tựa đề/ tóm tắt của bài báo của họ).

Hoặc xét theo đặc trưng thời gian của mạng, đồ thị mạng xã hội có thể được chia thành các chuỗi đồ thị khác nhau theo một bước thời gian nhất định. Đường trung bình động (moving average) là giá trị trung bình của giá trị phỏng đoán cho một cạnh trong một khoảng thời gian nhất định [13]. Bằng cách nhìn vào mức trung bình này qua nhiều thế hệ tiến hóa, người ta có thể đưa ra những dự đoán liên kết rất chính xác.

Hơn nữa, vấn đề dự đoán liên kết được nghiên cứu trong khung học có giám sát (supervised learning framework) bằng cách coi nó như một thể hiện của bài toán phân lớp nhị phân (binary classification problem). Các phương pháp này sử dụng các biện pháp tô-pô (topological) và ngữ nghĩa (semantic) được xác định giữa các nút làm đặc trưng cho các bộ phân lớp. Đưa ra một ảnh chụp nhanh (snapshots) của mạng xã hội tại thời điểm $t$ để huấn luyện, chúng coi tất cả các liên kết có mặt tại thời điểm $t$ là mẫu dương (positive samples) và coi một mẫu lớn các liên kết vắng mặt (cặp nút không được kết nối) tại thời điểm $t$ là mẫu âm (negative samples). Các bộ phân lớp đã học thực hiện nhất quán trên tất cả các tập dữ liệu, không giống như các phương pháp heuristic không nhất quán, mặc dù độ chính xác của dự đoán vẫn rất thấp [14].

Có một số lý do cho độ chính xác dự đoán thấp này. Một trong những lý do chính là độ lệch lớp rất lớn liên quan đến dự đoán liên kết. Trong các mạng lớn, không có gì lạ khi xác suất liên kết trước đó ở mức $10^{−4}$ trở xuống, điều này khiến cho vấn đề dự đoán trở nên rất khó khăn, dẫn đến hiệu suất kém. Ngoài ra, khi mạng phát triển theo thời gian, các liên kết tiêu cực tăng trưởng theo phương trình bậc hai trong khi các liên kết tích cực chỉ phát triển tuyến tính với các nút mới.

Tài liệu tham khảo

[1] http://www.cs.rpi.edu/~zaki/PaperDir/SNDA11.pdf

[2] An Algorithmic Approach to Social Networks - David Liben-Nowell - Phd thesis

[3] The Link Prediction Problem for Social Networks - David Liben-Nowell†, Jon Kleinberg

[4] Link Prediction in Complex Networks by Multi Degree Preferential-Attachment Indices - Ke Hu, Ju Xiang

[5] arxiv.org/abs/1111.4570 - Four Degrees of Separation

[6] Computationally Efficient Link Prediction in a Variety of Social Networks - MICHAEL FIRE, LENA TENENBOIM-CHEKINA, RAMI PUZIS, OFRIT LESSER,

[7] M. E. J. Newman. Clustering and preferential attachment in growing networks. Physical Review E, 64(025102), 2001.

[8] Robustness of Link-prediction Algorithm Based on Similarity and Application to Biological Networks - Liang Wang, Ke Hu and Yi Tang

[9] A Link Prediction Approach to Recommendations in Large-Scale User-Generated Content Systems - Nitin Chiluka, Nazareno Andrade, and Johan Pouwelse

[10] Scalable Proximity Estimation and Link Prediction in Online Social Networks - Han Hee Song Tae Won Cho Vacha Dave Yin Zhang Lili Qiu

[11] Using Friendship Ties and Family Circles for Link Prediction - Elena Zheleva and Lise Getoor

[12] Link Prediction and Recommendation across Heterogeneous Social Networks - Yuxiao Dong, Jie Tang, et al

[13] The Algorithm of Link Prediction on Social Network - Liyan Dong Yongli Li, Han Yin, Huang Le, and Mao Rui1

[14] Learning Algorithms for Link Prediction Based on Chance Constraints - Janardhan Rao Doppa ,JunYu

Powered by Hugo with Console Theme.