Thể tích Hessian và Basin

Khi thảo luận về “các lưu vực rộng (broad basins)” trong miền mất mát của một mạng DNN, Hessian của hàm mất mát thường được đề cập. Bài viết này sẽ tập trung giải thích một xấp xỉ lý thuyết đơn giản của thể tích lưu vực (basin volume) mà sử dụng Hessian của hàm mất mát. ¹ 1. Lưu ý rằng mô hình này không hề hoàn hảo và cũng không thể tính toán được đối với các mạng học lớn nếu không có thêm các thủ thuật/phép tính gần đúng!.

Giả sử rằng cực tiểu của chúng ta có giá trị mất mát $loss = 0$. Định nghĩa lưu vực (basin) như một vùng của không gian tham số mà rút về vị trí cực tiểu của ta trong đó $loss < \text{threshold } T$. ² 2. Việc đặt ra một ngưỡng không nhất thiết là một kỳ vọng hay một tiêu chuẩn, nhưng nó giúp việc thiết lập mô hình dễ dàng hơn.

Mô hình đơn giản nhất

Nếu tất cả các trị riêng của ma trận Hessian đều dương (positive) và không tầm thường (non-trivial) ³ 3. Điều kiện này cơ bản là không bao giờ xảy ra với các mạng học DNN; chúng ta sẽ xử lý một xíu để điều chỉnh vấn đề này trong phần kế tiếp. , ta có thể xấp xỉ giá trị hàm mất mát như một parabol được căn giữa dựa trên cực tiểu của ta như sau:

Hình 1. Phần parabol mà chúng ta thấy trên đồ thị chính xác là lưu vực của chúng ta, vì trục thẳng đứng bị cắt ở ngưỡng mất mát.

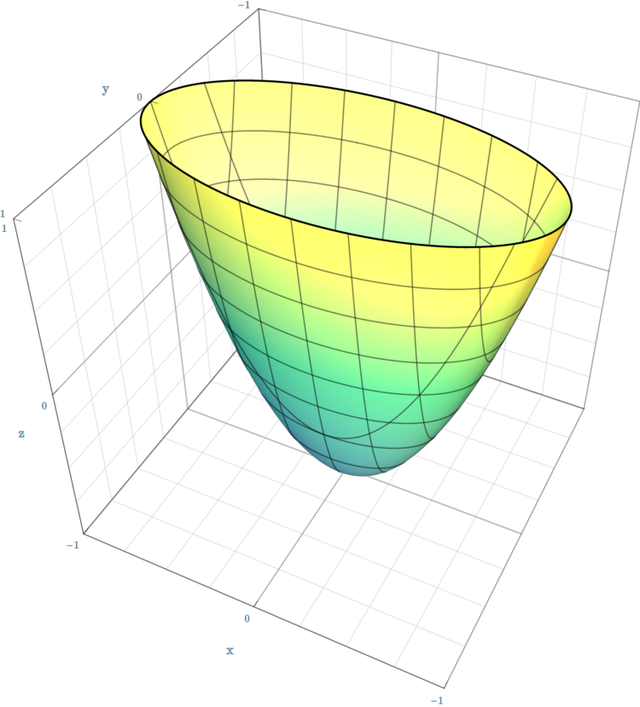
Trục dọc là mất mát, và mặt phẳng ngang là không gian tham số. Hình dạng của lưu vực trong không gian tham số là bóng của parabol này, là một hình elip.

Các hướng chính của độ cong của parabol được đưa ra bởi các vectơ riêng của Hessian. Độ cong (đạo hàm bậc hai) theo mỗi hướng đó được đưa ra bởi giá trị riêng tương ứng.

Bán kính (Radii) của hình elip: Nếu chúng ta bắt đầu ở cực tiểu và đi theo một hướng chính, mất mát lúc này như một hàm khoảng cách đã di chuyển được tính toán như sau: $$ L(x) = \frac{1}{2}\lambda_i x^2 $$ trong đó $\lambda_i$ là trị riêng Hessian theo hướng đó.

Thế nên với ngưỡng mất mát cho trước của ta $T$, ta sẽ chạm đến ngưỡng đó ở khoảng cách $$ x = \sqrt{\frac{2T}{\lambda_i}} $$ Đây là bán kính của hình elip lưu vực mất mát theo hướng đó.

Thể tích của hình elip được tính như sau: $$ V_{\text{basin}} = V_i\prod_i\sqrt{\frac{2T}{\lambda_i}} $$ trong đó hằng số $V_n$ là thể tích của quả cầu đơn vị trong không gian $n$ chiều. Bởi vì tích của các trị riêng là định thức của ma trận Hessian, nên ta có thể viết lại như sau: $$ V_{\text{basin}} = \frac{V_n(2T)^{n/2}}{\sqrt{\det[Hessian]}} $$

Vì vậy, thể tích lưu vực tỷ lệ nghịch với căn bậc hai của định thức của Hessian. Mọi thứ trong tử số đều là hằng số, vì vậy chỉ có định thức của Hessian là quan trọng trong mô hình này.

Và vấn đề ở đây là với mô hình này là định thức của Hessian thường bằng không, do các trị riêng bằng không.

Sửa lỗi mô hình

Nếu ta không thêm vào một thành phần chính quy hóa trong hàm mất mát, thì lưu vực như ta đã định nghĩa trước đó thực sự có thể vô cùng lớn (đây không chỉ là vấn đề với mô hình parabol mà còn là đối với nhiều mô hình khác nữa). Tuy nhiên, chúng ta không thực sự quan tâm đến thể tích quá xa gốc tọa độ mà nó không bao giờ đạt tới được.

Một cách có cơ sở để sửa mô hình là xem xét khối lượng được cân nhắc theo phân phối khởi tạo. Cách này dễ làm việc nhất nếu khởi tạo là Gaussian. Để làm cho phép tính dễ hiểu hơn, chúng ta có thể thay thế ellipsoid của mình bằng một “ellipsoid mờ” – tức là một hàm Gaussian đa biến (multivariate Gaussian). Bây giờ chúng ta chỉ cần lấy tích phân của tích của hai hàm Gaussian, điều này hẳn là dễ dàng. Và cũng có một số lý do có cơ sở để sử dụng một “ellipsoid mờ”, mà chúng ta sẽ không giải thích ở đây mà chúng ta sẽ thảo luận trong một bài viết khác (maybe).

Tuy nhiên, điều này chỉ có cơ sở và hợp lý một phần nào đấy. Nếu bạn suy nghĩ kỹ hơn về nó, nó bắt đầu trở nên không rõ ràng: Liệu rằng chúng ta nên sử dụng khởi tạo Gaussian hay ta nên dựa trên chuẩn L2? Còn những trường hợp chuẩn đạt đỉnh trong quá trình huấn luyện và nhỏ ở đầu và cuối quá trình thì sao?

Nếu ta có một chính quy hoá L2 trong hàm mất mát, thì vấn đề khối vô hạn thường biến mất. Thành phần chính quy L2 giúp các trị riêng luôn dương, dẫn đến biểu thức ổn định. Nếu ta dùng weight decay thì ta có diễn giải nó như thành phần chính quy L2 và thêm nó vào hàm mất mát!.

Để có một phép xấp xỉ tương đối đương giản, chúng tôi đề xuất biểu thức như sau: $$ V_{\text{basin}} = \frac{V_n(2T)^{n/2}}{\sqrt{\det[Hessian(Loss) + (\lambda +c)I_n]}} $$ trong đó:

• $Loss$ là hàm mất mát mà chưa có thành phần chính quy.
• $\lambda$ là lượng trọng số suy giảm (weight decay) (hoặc chính quy hóa L2 $\frac{1}{2}\lambda|\theta|^2$)
• $c = k / \sigma^2$, trong đó $\sigma$ là độ lệch chuẩn của Gaussian khởi tạo và $k$ là hằng số theo thứ tự đơn vị. Chúng tôi chưa tính toán chính xác được giá trị $k$ phù hợp nhất về mặt lý thuyết. Nhưng đối với một mô hình thô, $ k = 1$ có lẽ là đủ tốt rồi.
• $T$ là ngưỡng mất mát. Nếu bạn thực sự quan tâm đến thể tích tuyệt đối, bạn có thể thử đặt $T$ theo kinh nghiệm bằng cách xem xét nơi xấp xỉ parabol bị phá vỡ. Nếu bạn chỉ quan tâm đến thể tích so với các lưu vực khác, bạn có thể bỏ qua $T$ vì nó là hằng số.

Ước lượng trong thực hành

Nếu mạng nơ-ron sâu (DNN) mà ta quan tâm có kích thước lớn (ví dụ, >10k tham số), ma trận Hessian trở nên rất phức tạp. ⁵ 5. Tôi nghĩ việc tính toán trực tiếp các giá trị riêng và vector riêng có độ phức tạp là $O(n^3)$ . May mắn thay, có thể ước tính hiệu quả lượng $\det[Hessian(Loss) + (\lambda + c)I_n]$ mà không cần phải tính trực tiếp ma trận Hessian.

Một phương pháp đúng ⁷ 7. Phương pháp này chỉ hoạt động tốt nếu $(\lambda + c)$ lớn hơn đáng kể so với độ phân giải của phương pháp cầu phương Lanczos ngẫu nhiên. để thực hiện điều này là lấy phổ giá trị riêng của ma trận Hessian bằng cách sử dụng phương pháp cầu phương Lanczos ngẫu nhiên (stochastic Lanczos quadrature). Sau đó, dịch phổ trị riêng lên bởi lượng $λ + c$ và ước tính tích.

Một chút về các công trình gần đây

Cách “đơn giản” là sử dụng dấu vết (trace) của ma trận Hessian thay vì định thức (determinant). Đây là một cách cực kỳ dễ ước tính: chỉ cần lấy mẫu đạo hàm bậc hai theo các hướng ngẫu nhiên, và giá trị trung bình sẽ tỷ lệ với dấu vết. Vấn đề là dấu vết không phải là thước đo phù hợp và có lẽ là một đại diện kém chính xác cho định thức.

Hầu hết (hoặc tất cả?) các thước đo độ phẳng và thể tích mà tôi thấy trong tài liệu thực chất đều theo dõi dấu vết. Có một nghiên cứu (Keskar et. al.) ¹¹ 11. Bài báo này được trích dẫn rộng rãi và nhìn chung rất chất lượng. dường như điều chỉnh theo hướng không đúng (tăng ảnh hưởng của các giá trị riêng lớn so với dấu vết, trong khi đáng lẽ phải làm ngược lại). ¹² 12. Định thức là một tích, vì vậy nó nhạy cảm hơn với các giá trị riêng nhỏ so với dấu vết.

Có một nghiên cứu khác lấy mẫu bán kính elip trong các hướng ngẫu nhiên và tính thể tích của lát cắt elip theo hướng đó (tỷ lệ với $r^n$). Mặc dù về mặt kỹ thuật đây là một ước tính không chệch cho các elip hữu hạn, nhưng phương pháp này gặp hai vấn đề trong thực tế: ¹³ 13. Tôi đã xác nhận qua mô phỏng rằng phương pháp này có sai sót với $n$ rất lớn. Việc áp dụng điều chỉnh tương đương với $(\lambda+c)I_n$ có thể khắc phục vấn đề đầu tiên nhưng không giải quyết được vấn đề thứ hai.

• Elip thường thực sự là vô hạn, nghĩa là phương pháp này đang lấy mẫu để ước tính một lượng vô hạn. (Dễ đoán, ước tính trung vị tăng không giới hạn khi chúng ta tăng số lượng mẫu.)
• Có quá ít mẫu để ước tính chính xác định thức, và giá trị được theo dõi trên thực tế khá giống dấu vết.

Lý thuyết thông tin

Cần bao nhiêu bit để xác định (xác định vị trí) một lưu vực mất mát?

Câu trả lời đơn giản nhất là $−\log2(V)$, trong đó $V$ là thể tích được khởi tạo theo trọng số của lưu vực. Trọng số được thực hiện sao cho nó tích hợp thành 1.

Tài liệu tham khảo

Bài viết được dịch từ Hessian and Basin volume bởi Vivek Hebbar