Định lý Glivenko-Cantelli

Apr. 1, 2025

1. Động lực

Trong hầu hết thiết lập thống kê chung, chúng ta có một phân phối xác suất chưa biết $\mu$, và chúng ta cố gắng ước lượng các đặc tính của nó bằng cách lấy các mẫu độc lập (independent), đồng phân phối (identically distributed samples) $X_1, X_2, \ldots, X_n$ với phân phối $\mu$ (viết là $X_i \sim \mu$). Hy vọng là khi chúng ta lấy đủ số lượng mẫu ($n \to \infty$), chúng ta có thể khôi phục các đặc tính của phân phối $\mu$. Ví dụ, Luật số lớn mạnh (Strong Law of Large Numbers) phát biểu rằng, với xác suất bằng 1, trung bình mẫu của dữ liệu của chúng ta hội tụ đến trung bình thực của phân phối (true average of the distribution) $\mu$:

$$ \mathbb{P} _\mu \left( \lim _{n\to\infty} \frac{1}{n} \sum _{i=1}^n X_i = \mathbb{E} _\mu[X_1] \right) = 1. $$

Định lý này cũng đúng cho bất kỳ hàm $f(X_i)$ nào của dữ liệu của chúng ta, miễn là $\mathbb{E}[|f(X_1)|] < \infty$.

Theo trực giác, hy vọng và giả định chung của thống kê là có thể ước lượng nhất quán bất kỳ đặc tính nào của phân phối $\mu$. Một phân phối $\mu$ trên $\mathbb{R}$ xác định một hàm phân phối tích lũy (cumulative distribution function - CDF) $$ F_\mu(t) := \mathbb{P}_\mu(X \leq t). $$

CDF cũng xác định duy nhất phân phối mà nó phát sinh từ đó. Chúng ta có $\mu((a, b]) = F_\mu(b) - F_\mu(a)$, điều này xác định giá trị của $\mu$ theo cấu trúc đo ngoài Carathéodory (Carathéodory outer measure construction). Vì vậy, nếu chúng ta có thể ước lượng nhất quán $F_\mu$ với dữ liệu $X_1, \ldots, X_n$ khi $n \to \infty$, chúng ta sẽ có thể ước lượng bất kỳ đặc tính nào của phân phối $\mu$. Định lý Glivenko-Cantelli nói rằng việc ước lượng toàn bộ phân phối này thực sự là khả thi.

2. Phát biểu Định lý Glivenko-Cantelli

Đầu tiên, chúng ta đề cập đến bộ ước lượng của $F_\mu$ nên là gì.

Định nghĩa 2.1: Hàm phân phối tích lũy theo mẫu hoặc thực nghiệm (sample or empirical CDF) là $$ F_{\mu_n}(t) := \frac{1}{n} \sum_{i=1}^n \mathbf{1}_{(-\infty,t]}(X_i). $$ Đây là một hàm không giảm (nondecreasing), liên tục bên phải (right continuous function), tăng lên $1/n$ mỗi khi chúng ta gặp bất kỳ giá trị $X_i$ nào.

Ví dụ 2.1: Nếu $\mu$ là phân phối đều trên $[0, 1]$, $F_\mu(t) = t$ với $t \in [0, 1]$. Đây là một so sánh về hình dạng của CDF thực nghiệm $F_{\mu_n}$ so với $F_\mu$ cho $n = 10$ và $n = 100$ mẫu.

Picture taken from chapter 4 of Martin J. Wainwright. High-Dimensional Statistics: A Non-Asymptotic Viewpoint. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, 2019.

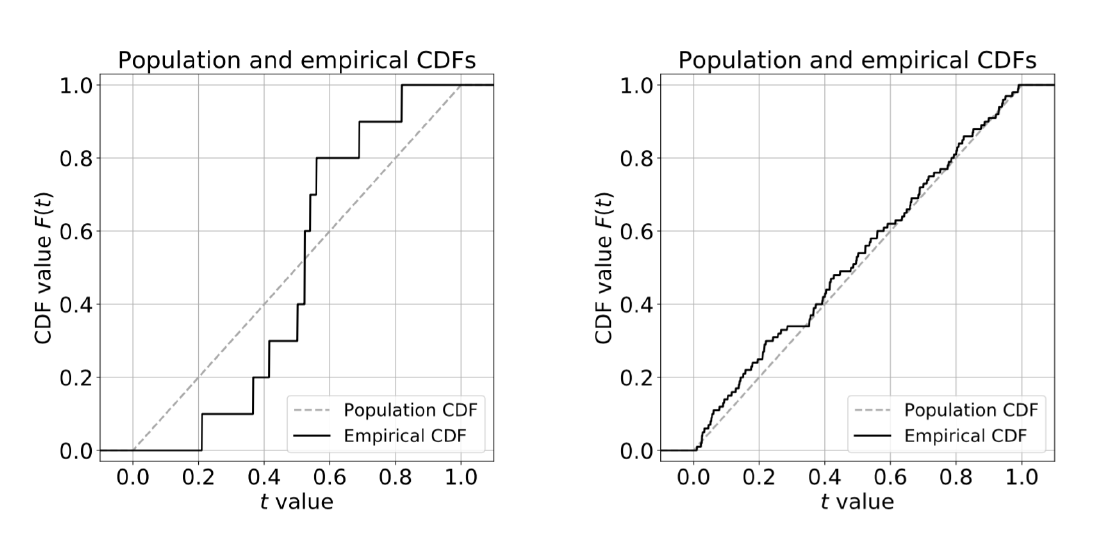
Việc tiếp theo cần làm là xác định loại hội tụ hàm mà chúng ta sẽ đề cập khi thảo luận về tính nhất quán. Đáng ngạc nhiên, hội tụ này là hội tụ đều (uniform), về cơ bản là dạng hội tụ mạnh nhất mà người ta có thể hy vọng.

Định lý 2.2 (Glivenko-Cantelli):

Cho $\mu$ là một phân phối trên $\mathbb{R}$, và $X _1, X _2, \ldots \stackrel{iid}{\sim} \mu$, và $F _{\mu _n} = \frac{1}{n}\sum _{i=1}^n \mathbf{1} _{(-\infty,t]}(X_i)$. Khi $n \to \infty$,

$$ \sup_{t\in\mathbb{R}} |F _{\mu_n}(t) - F _\mu(t)| \stackrel{a.s.}{\longrightarrow} 0. $$

3. Chứng minh Định lý Glivenko-Cantelli

Đầu tiên, chúng ta cần chứng minh một bổ đề tất định như sau:

Bổ đề 3.1:

Cho $F_n$ và $F$ là các hàm bị chặn đều (uniformly bounded), không giảm (nondecreasing) và liên tục bên phải (right-continuous). Nếu

$F_n(t) \to F(t)$ với mọi số hữu tỷ $t$
$F_n(t) \to F(t)$ với mọi nguyên tử của $F$ (những điểm mà $F(t) \neq \lim_{s\uparrow t} F(s)$),

thì $\sup_{t\in\mathbb{R}} |F_n(t) - F(t)| \xrightarrow{n\to\infty} 0$.

Đây là chứng minh của bổ đề trong trường hợp $F$ không có nguyên tử; trường hợp tổng quát cũng tương tự, nhưng việc xây dựng $\varepsilon$-net trong chứng minh phức tạp hơn về mặt ký hiệu, nên chúng tôi bỏ qua.

Chứng minh Bổ đề 3.1:

Cho $\varepsilon > 0$. Tồn tại một mạng hữu hạn $T = {t_1 < \cdots < t_\ell}$ gồm các số hữu tỷ và nguyên tử của $F$ sao cho với mọi $t \in \mathbb{R}$, tồn tại $t’ \in T$ với $t’ > t$ và $F(t’) - F(t) < \varepsilon$. Trong trường hợp $F$ không có nguyên tử, chúng ta có thể đặt $t_j = \sup{x \in \mathbb{R} : F(x) \leq j/N}$ với $1 \leq j \leq N$.

Bây giờ, với mọi $t \in \mathbb{R}$, giả sử $t_j \in T$ là phần tử nhỏ nhất của $T$ mà $\geq t$, chúng ta có $$ \begin{equation} |F_n(t) - F(t)| \leq \begin{cases} F_n(t_j) - F(t_{j-1}) & \text{nếu } F_n(t) \geq F(t) \\ F(t_j) - F_n(t_{j-1}) & \text{nếu } F_n(t) < F(t) \end{cases} \end{equation} $$

Hay $$ \begin{equation} |F_n(t) - F(t)| \leq \begin{cases} |F_n(t_j) - F(t_j)| + |F(t_j) - F(t_{j-1})| & \text{nếu } F_n(t) \geq F(t) \\ |F(t_j) - F(t_{j-1})| + |F(t_{j-1}) - F_n(t_{j-1})| & \text{nếu } F_n(t) < F(t) \end{cases} \end{equation} $$

Chọn $n$ đủ lớn sao cho $|F_n(t’) - F(t’)| < \varepsilon$ với mọi $t’ \in T$, tức là $< 2\varepsilon$.

Vậy, với $n$ đủ lớn, $\sup_{t\in\mathbb{R}} |F_n(t) - F(t)| < 2\varepsilon$. Cho $\varepsilon \downarrow 0$. Chứng minh hoàn tất.

Bây giờ, đây là chứng minh của định lý Glivenko-Cantelli.

Chứng minh Định lý 2.2 (Glivenko-Cantelli):

Với một $t$ cố định, Luật số lớn mạnh cho rằng $$ \begin{equation} \frac{1}{n} \sum_{i=1}^n \mathbf{1} _{(-\infty,t]}(X_i) \stackrel{a.s.}{\longrightarrow} \mathbb{E} _\mu[\mathbf{1} _{(-\infty,t]}(X_i)] = \mathbb{P} _\mu(X_1 \leq t). \end{equation} $$

Tức là, $F_{\mu_n}(t) \to F_\mu(t)$ với xác suất bằng 1. Vậy nếu chúng ta đặt $S = \mathbb{Q} \cup \{ \text{các nguyên tử của } F_\mu \}$, sự hội tụ xảy ra với xác suất bằng 1 cho mỗi trong số đếm được các điểm trong $S$, nên $$ \begin{equation} \mathbb{P} _\mu(F _{\mu_n}(t) \to F _\mu(t) ; \forall t \in S) = 1. \end{equation} $$

Do đó, theo bổ đề, $$ \begin{equation} \mathbb{P} _\mu\left(\sup _{t\in\mathbb{R}} |F _{\mu_n}(t) - F _\mu(t)| \xrightarrow{n\to\infty} 0 \right) = 1. \end{equation} $$

Có hai điều quan trọng cần lưu ý về chứng minh này:

Chứng minh không cung cấp bất kỳ thông tin nào về tốc độ hội tụ của $F_{\mu_n}$ đến $F_\mu$.
Chứng minh phụ thuộc nhiều vào thứ tự tuyến tính của $\mathbb{R}$, nên khó tổng quát hóa cho, chẳng hạn, $\mathbb{R}^n$.

Khái niệm kích thước VC sẽ giải quyết cả hai vấn đề này.