Biến đổi Laplace và Fourier

Đây là một bài viết ngắn thảo luận về mối quan hệ giữa biến đổi Laplace và biến đổi Fourier, hai công cụ quan trọng trong toán học kỹ thuật.

Biến đổi Fourier

Biến đổi Fourier của một hàm \(x(t)\) được định nghĩa như sau:

$$ X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-i\omega t} , dt $$

Giả sử chúng ta có một hàm \(x(t) = e^{-k t} \sin(\Omega t)\). Khi đó, biến đổi Fourier của nó được tìm thấy là:

$$ X(\omega) = \frac{\Omega}{\omega^2 + \Omega^2} $$

Chú ý rằng hàm này phân kỳ tại các điểm \(\omega = \pm \Omega\). Do đó, biến đổi Fourier cho chúng ta biết rằng hàm có một hình sin ở đâu đó với tần số góc \(\Omega \) (điều mà chúng ta đã biết, tất nhiên, vì chúng ta đã biết hàm từ trước).

{: .definition}

Biến đổi Fourier cho chúng ta biết các tần số góc \(\omega_i\) của tất cả các hình sin có trong một hàm \(x(t)\).

Dưới đây là đồ thị độ lớn của biến đổi Fourier của \(x(t) = e^{-0.5 t} sin(2t)\), được tạo ra bằng MATLAB.

Biến đổi Laplace

Biến đổi Laplace của một hàm \(x(t)\) được định nghĩa như sau:

$$ \mathcal{L}{x(t)} = \int_{0}^{\infty} x(t) e^{-s t} , dt $$

trong đó \(s\) là một số phức, với:

$$ s = \alpha + i \omega $$

Thay thế dạng này của \(s\) vào công thức biến đổi Laplace, chúng ta có:

$$ \mathcal{L}{x(t)} = \int_{0}^{\infty} x(t) e^{-i \omega t} e^{- \alpha t} , dt $$

Chú ý rằng công thức này giờ đây gần như giống hệt với công thức chúng ta đã có cho biến đổi Fourier của \(x(t)\)! Sử dụng \(x(t) = e^{-k t} \sin(\Omega t)\), như chúng ta đã có trước đó, chúng ta có thể tính toán tích phân và nhận thấy rằng:

$$ \mathcal{L}{x(t)} = \frac{\Omega}{(k + \alpha + i \omega)^2 + \Omega^2} $$

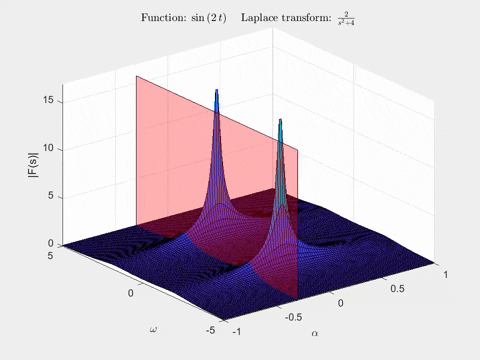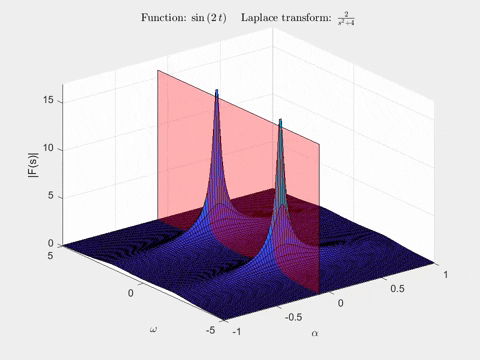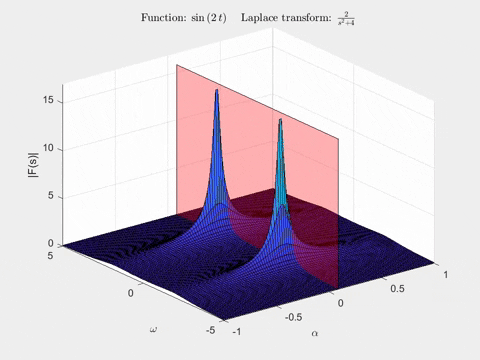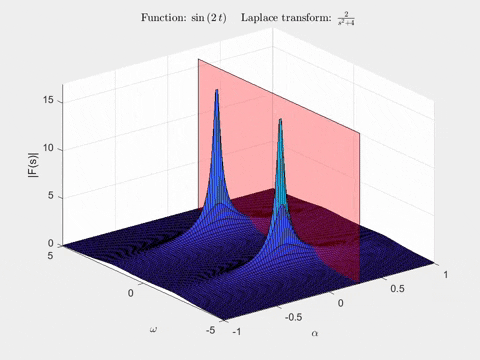
Để hình dung biến đổi Laplace, chúng ta có thể sử dụng đồ thị 3D, với hai trục đầu tiên tương ứng với \(\alpha = \text{Re}(s)\) và \(\omega = \text{Im}(s)\), và chiều cao của đồ thị được đặt là \(|\mathcal{L}{x(t)}| = |F(s)|\) (một ký hiệu khác cho biến đổi Laplace). Lưu ý rằng ở đây chúng ta chỉ vẽ độ lớn của biến đổi Laplace. Đối với hàm \(x(t) = e^{-0.5 t} sin(2t)\), biến đổi Laplace trông như thế này:

Bằng cách phân tích mẫu số của hàm này, chúng ta có thể thấy các cực sẽ xuất hiện tại tọa độ \((\alpha, \omega) = (-0.5, \pm 2)\). Không chỉ chúng ta được cung cấp thông tin về các hình sin hiện diện, mà bây giờ chúng ta cũng biết hệ số của thừa số mũ, từ giá trị của \(\alpha \) tại các cực!

Định nghĩa 1: Các cực của biến đổi Laplace \(\mathcal{L}{x(t)}\) cho chúng ta biết về các hàm mũ và hình sin có trong một hàm \(x(t)\).

Hai phép biến đổi này có mối quan hệ như thế nào?

Khi bạn tính toán đồ thị 2D của biến đổi Fourier của một hàm, bạn thực sự đang lấy một lát cắt 2D của biến đổi Laplace của hàm đó. Hãy quay lại dạng của biến đổi Laplace mà chúng ta đã có trước đó:

$$ \mathcal{L}{x(t)} = \int_{0}^{\infty} x(t) e^{-i \omega t} e^{- \alpha t} , dt $$

Nếu chúng ta đặt $$ \alpha $$ bằng không, phép biến đổi này chỉ đơn giản thu gọn thành \(X(\omega)\), biến đổi Fourier của \(x(t)\). Vì vậy, biến đổi Fourier của một hàm chỉ là biến đổi Laplace cho \(\alpha = 0\), trong đó \(s = \alpha + i \omega\).

Thực tế, tất cả những gì biến đổi Laplace đang làm là liên tục tìm biến đổi Fourier của một hàm đã được sửa đổi \(x(t, \alpha) = x(t) e^{-\alpha t}\). Mỗi lần, chúng ta điều chỉnh \(\alpha\) một lượng nhỏ, sau đó tính lại biến đổi Fourier và vẽ độ lớn của nó! Tôi sẽ cho bạn xem hai hoạt ảnh minh họa điều này.

Hoạt ảnh đầu tiên cho thấy biến đổi Fourier của \(e^{-\alpha t} \sin(2t)\), với \(\alpha\) thay đổi. Bạn có thể nhận thấy sự tương đồng giữa hình dạng thay đổi của biến đổi Fourier và hình dạng của các cực biến đổi Laplace mà chúng ta đã thấy trước đó không?

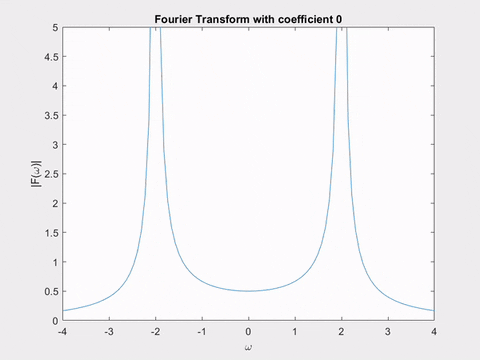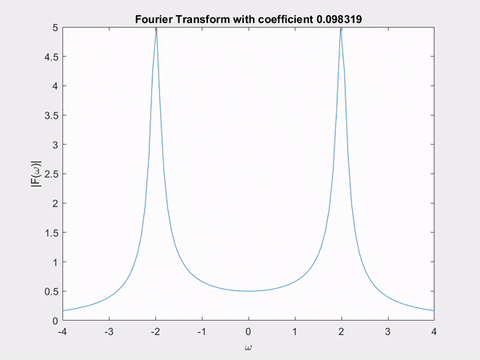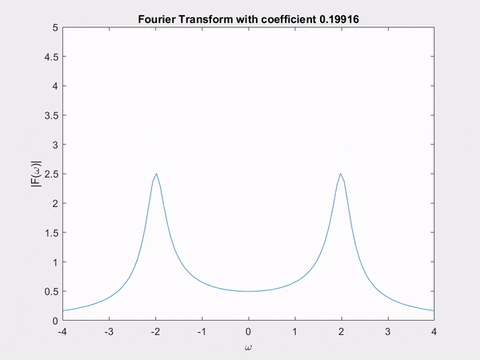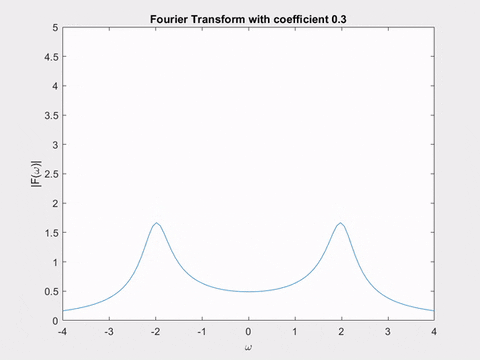
Hoạt ảnh thứ hai cho thấy một mặt phẳng trong biến đổi Laplace của \(sin(2t)\). Khi chúng ta di chuyển nó, hãy chú ý hình dạng của đường cong được tạo ra bởi giao điểm của mặt phẳng với bề mặt của biến đổi Laplace - nó chính xác là biến đổi Fourier mà chúng ta vừa thấy trong hoạt ảnh!